Решение:
Схема исследования функции на экстремум.
1. Находим интервалы монотонности.
Необходимое условие существования экстремума - наличие у функции критических (стационарных) точек. Найдем критические (стационарные) точки, для этого найдем первую производную и приравняем ее к нулю $$y' = ( x^3-6x^2-15x-8)'= 3x^2-12x-15 $$ приравняем к 0 $$ 3x^2-12x-15= 0 => x_1= -1; \quad x_2 = 5$$ функция имеет две критические (стационарные) точки.
2. Находим интервалы монотонности.
Функция имеет две критические точки, они делят ось Ox (ОДЗ) на три интервала монотонности.
интервал \((-\infty; -1)\) найдем значение первой производной в любой точке интервала \(f(-2) = (x+1)(x-5) > 0\), на этом интервале функция возрастает.
интервал \(( -1; 5)\) найдем значение первой производной в любой точке интервала \(f(0) = (x+1)(x-5) < 0\), на этом интервале функция убывает.
интервал \(( 5; +\infty)\) найдем значение первой производной в любой точке интервала \(f(6) = (x+1)(x-5) > 0\), на этом интервале функция возрастает.
3. Экстремумы функции.
Достаточным условием существования экстремума является изменение знака производной при переходе через критическую точку, рассмотрим критические точки
\(x = -1\): \(\quad + \quad 0 \quad -\), т.е. функция имеет точку максимума с координатами \((-1;0)\)
\(x = 5\): \(\quad - \quad 0 \quad +\), т.е. функция имеет точку минимума с координатами \((5;-108)\)
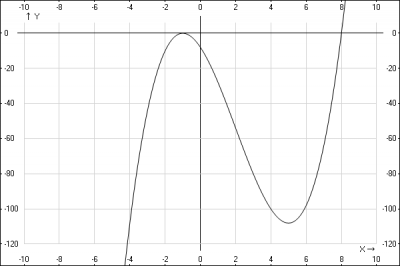
График функции: