Данная задача сводится к определению допустимого диапазона знпчений параметра \( a \).Проведем преобразование уравнения
$$ \frac{1-2а\sqrt{1+х^2} +а*(1+х^2)}{(1+х^2)-2\sqrt{1+х^2}}=3 => \begin{cases} 1-2а\sqrt{1+х^2} +а*(1+х^2) =3*(1+х^2)-6\sqrt{1+х^2} \\ (1+х^2)-2\sqrt{1+х^2} \ne 0 \end{cases} $$
$$ \begin{cases} (1+х^2)(a-3) -2\sqrt{1+х^2}(a-3) +1 = 0 \\ (1+х^2) \ne 2\sqrt{1+х^2} \end{cases} =>$$решим квадратное уравнение относительно \( \sqrt{1+x^2}\)$$\begin{cases} \sqrt{1+x^2}_{1,2} = \frac{2*(a-3) \pm \sqrt{4(a-3)^2 - 4*(a-3)}}{2*(a-3)} \\ 1+х^2 \ne 4 \end{cases} => \begin{cases} \sqrt{1+x^2}_{1,2} =1 \pm \sqrt{\frac{a-4}{a-3}} \\ a \ne 3 \\ х \ne \pm \sqrt{3} \end{cases}$$получили решение квадратного равнения, но в решении два корня, поэтому необходимо установить ОДЗ $$ \begin{cases} \frac{a-4}{a-3} \geq 0 \\ 1 - \sqrt{\frac{a-4}{a-3}} \geq 0 \end{cases} => \begin{cases} (a-4)(a-3) \geq 0 \\ a \ne 3\\ 1 \geq \frac{a-4}{a-3} \end{cases}$$$$\begin{cases} (a-4)(a-3) \geq 0 \\ a \ne 3\\ 0 \geq \frac{a-4 -a +3 }{a-3} \end{cases} => \begin{cases} (a-4)(a-3) \geq 0 \\ a \ne 3\\ 0 \geq -\frac{1 }{a-3} \end{cases}$$$$ \begin{cases} (a-4)(a-3) \geq 0 \\ a \ne 3\\ a-3 > 0 \end{cases}$$при помощи метода змейки определяем допустимый диапазон \( a \)
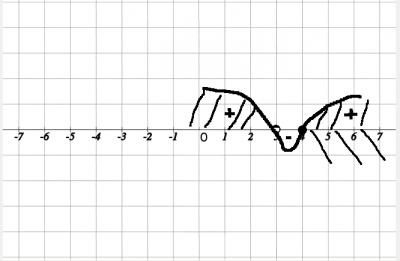
Ответ: при значении параметра \( a \cup [4; +\infty)\) уравнение будет иметь хотябы одно решение.



