Решение: объем пирамиды ищется по формуле $$V = \frac{1}{3}S_{осн}H \quad (1)$$
1. Найдем площадь основания.
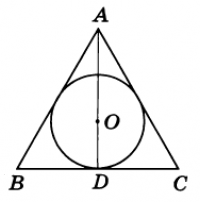
В основании лежит правильный треугольник, в который вписан круг. Воспользуемся свойством медианы, высоты и биссектрисы правильного треугольника они совпадают - \(AD\). Согласно свойства медианы - в точке пересечения они делятся в отношении \(2:1\) и центр вписанной окружности лежит в точке пересечения медиан, т.е. \(OD = r => AD = 3OD = 3r = h\). Для нахождения площади нужна еще сторона. Пусть сторона равна \(a\), тогда высота правильного треугольника равна $$h = \frac{\sqrt{3}}{2}a = 3r => a = \frac{6r}{\sqrt{3}}$$ Тогда площадь основания равна $$S_{осн} = \frac{1}{2}ah =\frac{1}{2}\frac{6r}{\sqrt{3}}3r = \frac{9r^2}{\sqrt{3}}$$
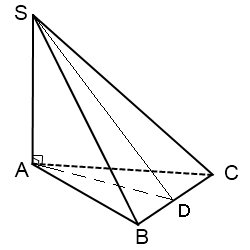
2. Найдем высоту пирамиды. Рассмотрим треугольник \(ΔDAS\) - по условию это прямоугольный треугольник с углом \(\angle SDC = 60^0\) и известной стороной \(AD\), тогда $$H = AD*tg(60^0) =>H = 3r*\sqrt{3}$$
3. Находим объем пирамиды. Подставляем результаты п.1,п.2 в (1) $$V = \frac{1}{3}S_{осн}H = \frac{1}{3}\frac{9r^2}{\sqrt{3}}3r*\sqrt{3} = 9r^3 = 1944 \text{ см}^3$$
Ответ: объем пирамиды равен \(V = 1944 \text{ см}^3\)



