
0 Голосов

|
 |
| Posted Март 13, 2013 by Вячеслав Моргун |
|
|
- Исследуем функцию при помощи первой производной. Результатом данного исследования должны стать стационарные точки (если есть) и интервалы монотонности.
- Найдем стационарные (критические) точки и интервалы монотонности. Для этого найдем первую производную и приравняем ее к 0 $$ f(x) = (x^3- x^4)' = 3x^2 - 4x^3 = 0 =>$$$$x^2(3 - 4x) = 0 => x_1=0; x_2=\frac{3}{4}$$необходимым условием существования экстремумов является равенство первой производной 0, достаточным условием существования экстремумов является смена знака производной при прохождении через стационарную точку.
- \( x = 0\), возьмем точки справа и слева от \( x \) и посчитаем производную
\( (-\infty; 0)\) - \(f'(-1) = x^2(3 - 4x) = (-1)^2*(3+4) > 0\) - т.к. производная больше нуля, на этом интервале функция возрастает
\( (0; \frac{3}{4})\) - \(f'(\frac{1}{2}) = x^2(3 - 4x) = (\frac{1}{2})^2*(3-\frac{4}{2}) > 0\), производная больше нуля, на этом интервале функция возрастает. Точка \( x = 0\) является стационарной, но производная знак не поменяла, т.е. это точка не является экстремумом - это точка перегиба.
- \( x = \frac{3}{4}\), возьмем точки справа и слева от \( x \) и посчитаем производную
\( (0; \frac{3}{4})\) - \(f'(\frac{1}{2}) = x^2(3 - 4x) = (\frac{1}{2})^2*(3-\frac{4}{2}) > 0\), т.к. производная больше 0, функция возрастает
\( (\frac{3}{4}; +\infty)\) - \(f'(2) = x^2(3 - 4x) = (2^2*(3-4*2) < 0\), т.к. производная меньше 0, функция убывает на данном интервале. Точка \( x = \frac{3}{4}\) является стационарной, производная знак поменяла с "+" на "-", т.е. это точка является экстремумом - это точка максимума.
- Исследуем функцию при помощи второй производной. Результатом данного исследования должны стать интервалы выпуклости. Найдем вторую производную, приравняем ее к 0 и найдем знак второй производной $$''f(x) = (f'(x))' = (3x^2 - 4x^3)' = 6x - 12x^2 = 0 =>x (1 - 2x) = 0 => x_1=0; x_2 = \frac{1}{2} $$получили две точки, в которых функция меняет выпуклость. Найдем знак второй производной
- \( x = 0\), возьмем точки справа и слева от \( x \) и посчитаем вторую производную
\( (-\infty; 0)\) - \(f''(-1) = x(1 - 2x) = (-1)*(1+2) < 0\) - т.к. вторая производная меньше нуля, на этом интервале функция выпукла вверх
\( (0; \frac{1}{2})\) - \(f''(\frac{1}{4}) = x*(1 - 2x) = (\frac{1}{4})^2*(1-\frac{2}{4}) > 0\), вторая производная больше нуля, на этом интервале функция выпукла вниз.
- \( x = \frac{1}{2}\), возьмем точки справа и слева от \( x \) и посчитаем вторую производную
\( (0; \frac{1}{2})\) - \(f''(\frac{1}{4}) = x*(1 - 2x) = (\frac{1}{4})^2*(1-\frac{2}{4}) > 0\), вторая производная больше нуля, на этом интервале функция выпукла вниз.
\( (\frac{1}{2}); +\infty\) - \(f''(1) = x*(1 - 2x) = 1*(1-2*1) < 0\), вторая производная меньше нуля, на этом интервале функция выпукла вверх.
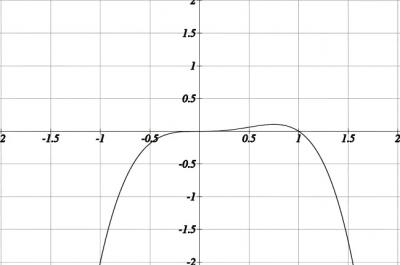
На рис. представлен график функции \( f(x) = x^3- x^4 \)
|
|



