Решение: найдем полную площадь поверхности пирамиды. Рассмотрим рисунок $$S_{полн} = S_{ABC} + S_{ASB} + S_{ASC} +S_{BSC} \quad (1) $$
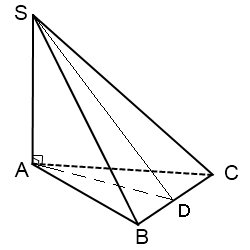
1. Площадь треугольников \(ΔASB\) и \(ΔASC\).
Треугольники \(ΔASB\) и \(ΔASC\) прямоугольные и равные (сторона \(AS\) общая, а стороны \(AB = AC =a\) т.к треугольник \(ΔABC\) - правильный по условию задачи), т.е. \(S_{ASB} = S_{ASC} = \frac{1}{2}AS*a\).
2. Площадь правильного треугольника \(S_{ABC} = \frac{\sqrt{3}}{4}a^2\).
3. Площадь треугольника \(ΔBSC\).
Треугольник \(ΔABC\) является проекцией треугольника \(ΔBSC\) на площадь основания. Угол между плоскостью этого треугольника \(ΔBSC\) и основанием равен \(60^0\), т.е. \(S_{ABC} = S_{BSC}*\cos(60^0) => S_{BSC} = 2S_{ABC}\)
4. Найдем сторону \(a\) правильного треугольника \(ΔABC\).
Треугольник \(ΔBSC\) - равнобедренный треугольник \(BS = SC\), тогда \(SD\) - высота, медиана этого треугольника, а угол \(\angle SDA = 60^0\). Из \(ΔABC\) высота правильного треугольника равна \(AD = \frac{\sqrt{3}}{2}a\), тогда из \(ΔASD\) найдем \(a\), \( tg(60^0) = \frac{AS}{AD} => AD = \frac{24}{\sqrt{3}}\), подставляем значение \(AD\), получаем \(\frac{\sqrt{3}}{2}a = \frac{24}{\sqrt{3}} => a = 16\).
5.Подставляем полученные результаты в (1) $$S_{полн} = S_{ABC} + 2S_{ASB} +2S_{ABC} => $$$$S_{полн} = 3S_{ABC} + 2S_{ASB} => S_{полн} = 3\frac{\sqrt{3}}{4}a^2 + 2\frac{1}{2}AS*a =>$$$$S_{полн} = 3\frac{\sqrt{3}}{4}16^2 + 24*16 = 192 + 384\sqrt{3} = 192(2+\sqrt{3})$$
Ответ: площадь полной поверхности пирамиды равна \(S_{полн} = 192(2+\sqrt{3})\)



