а) найдем коэффициент \(A\)
Воспользуемся свойством плотности распределения для нахождения параметра \(A\). Если все возможные значения плотности распределения принадлежат отрезку \([a;b]\), тогда \(\int_a^bf(x)dx = 1\). В нашем случае все значения попадают в интеграл \([-\frac{\pi}{2};\frac{\pi}{2}]\), получаем $$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}A\cos(x)dx = 1 => A\sin(\frac{\pi}{2}) - A\sin(-\frac{\pi}{2}) =1 => A = \frac{1}{2}$$
Ответ: коэффициент \(A = \frac{1}{2}\)
Найдем функцию распределения \(F(x)\). Для решения задачи воспользуемся формулой \( \int_{-\infty}^{x}f(t)dt = F(x)\).
Функцию распределения будем искать на трех интервалах.
1. \( x < -\frac{\pi}{2} \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{x}0dt = 0$$
2. \( -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{-\frac{\pi}{2}}f(t)dt + \int_{-\frac{\pi}{2}}^{ x}f(t)dt = $$$$ = \int_{-\infty}^{-\frac{\pi}{2}}0dt + \int_{-\frac{\pi}{2}}^{x}\frac{1}{2}\cos(t)dt = 0 + \frac{1}{2}\sin(x) +\frac{1}{2} = \frac{1}{2}(\sin(x)+1)$$
3. \( \frac{\pi}{2} < x \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{-\frac{\pi}{2}}f(t)dt + \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}f(t)dt + \int_{\frac{\pi}{2}}^{\infty}f(t)dt = $$$$ = \int_{-\infty}^{-\frac{\pi}{2}}0dt + \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1}{2}\cos(t)dt + \int_{\frac{\pi}{2}}^{x}0dt = $$$$ = 0 + \frac{1}{2} + \frac{1}{2} + 0 = 1$$
Ответ: функция распределения имеет вид: $$ F(x) = \begin{cases}0 & x < -\frac{\pi}{2}\\ \frac{1}{2}(\sin(x)+1) & -\frac{\pi}{2} \leq x \leq \frac{\pi}{2} \\ \\ 1 & \frac{\pi}{2} < x \end{cases} $$
б) построить график плотности распределения \(f(x)\)
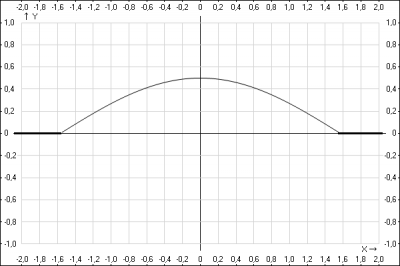
с) найти вероятность попадания случайной величины \(X\) в интервал \((-\frac{\pi}{2};\frac{\pi}{2})\)
Вероятность попадания случайной величины \(X\) в интервал \((a;b)\) равна определенному интегралу от плотности распределения \(f(x)\) по отрезку \((a;b)\), т.е. \(P(a < X < b)\int_a^bf(x)dx\) получаем $$P(-\frac{\pi}{2} < X < \frac{\pi}{2}) = \int_{-\frac{\pi}{2}}^{ \frac{\pi}{2}}\frac{1}{2}\cos(x)dx = >$$$$P(-\frac{\pi}{2} < X < \frac{\pi}{2}) = \frac{1}{2}\sin(x)|_{-\frac{\pi}{2}}^{\frac{\pi}{2}} = 1$$
Ответ: вероятность попадания случайной величины \(X\) в интервал \((\frac{\pi}{2};\frac{\pi}{2})\) равна \(P(-\frac{\pi}{2} < X < \frac{\pi}{2}) = 1\)





