Знайти об'єм конуса. Площа бічної поверхні крнуса дорівнює $240\pi \text{ см}^2$.

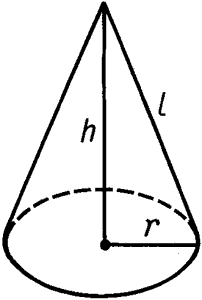
Решение: объем конуса равен

$$V = \frac{1}{3}S_{осн}h = \frac{1}{3}\pi r^2h \quad (1)$$ Радиус известен из условия $r = 12 \text{см}$ Нам необходимо найти высоту конуса. В условии дана площадь боковой поверхности, которая находится по формуле $$S_{бок} = \pi rl = 240\pi => l = \frac{S_{бок}}{\pi r} = \frac{240\pi}{12\pi} = 20$$ Из рисунка видно, что высоту можно найти по теореме Пифагора $$l^2 = h^2 + r^2 =>$$ $$h = \sqrt{l^2 - r^2} = \sqrt{ 20^2 - 12^2} = 16$$ Полученный результат подставляем в формулу объема (1), получаем $$V = \frac{1}{3}\pi r^2h = \frac{1}{3}\pi *12^2*16 = 768\pi$$
Ответ: объем конуса равен $V =  768\pi \text{ см}^3$