Решение: рассмотрим рисунок.
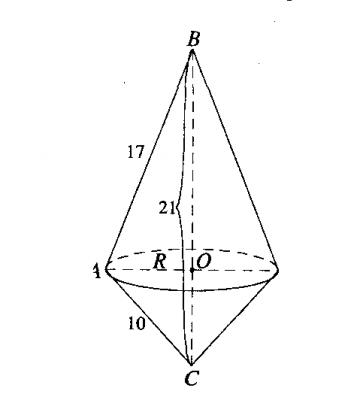
В результате вращения получаем фигуру, которую можно представить как сумму двух конусов с общим основанием.
Как известно объем конуса равен $$V = \frac{1}{3}S_{осн}h$$ тогда объем фигуры вращения равен $$V = V_1+ V_2 = \frac{1}{3}S_{осн}h_1 + \frac{1}{3}S_{осн}h_2 = \frac{1}{3}S_{осн}(h_1 + h_2) \quad (1)$$ Из условия задачи мы помним, что вращение происходит вокруг наибольшей стороны, т.е. \(h_1 = OB\), \(h_2 = OC\), \(h_1+h_2 = BC = 21\), подставляем в (1) $$V = \frac{1}{3}\pi R^2*21 = 7\pi R^2 \quad (2)$$ Теперь осталось найти радиус \(R = OA\).
Найдем радиус основания.
Рассмотрим треугольник \(ΔABC\). Опустим высоту из точки \(A\) на сторону \(BC\) в точку \(O\), получим \(R = OA\). Обозначим \(OC = x\), тогда из теоремы Пифагора из треугольников \(ΔBOA\) и \(ΔСOA\) получим $$\begin{cases}OA^2 + OB^2 = AB^2 \\ OC^2 + OA^2 = AC^2\end{cases} => \begin{cases}R^2 + (BC-OC)^2 = AB^2 \\ OC^2 + R^2 = AC^2\end{cases} => $$$$ \begin{cases}R^2 + (21-x)^2 = 17^2 \\ x^2 + R^2 = 10^2\end{cases} => \begin{cases}R^2 + 21^2 -42x + x^2 = 17^2 \\ x^2 + R^2 = 10^2\end{cases} => $$$$ \begin{cases}10^2 + 21^2 -42x = 17^2 \\ x^2 + R^2 = 10^2\end{cases} =>=>\begin{cases} x = 6 \\ R = 8\end{cases} $$ Подставляем результат в формулу объема (2) $$V = 7\pi R^2 = 7\pi 64 = 448\pi \text{см}^3$$
Ответ: объем тела вращения равен \(V = 448\pi \text{см}^3\)



