Решение:
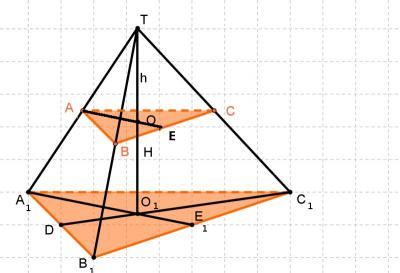
Данная задача на подобие двух тел. Необходимо найти коэффициент подобия и на основании его рассчитать объем.
Рассмотрим решение задачи на примере треугольной пирамиды.
Найдем закономерности, а затем проанализируем результат для произвольной пирамиды.
Как известно объем пирамиды равен $$ V = \frac{1}{3}S_{oc}*h $$ где \( S_{oc}\) - площадь основания пирамиды,
а \( h \) - высота пирамиды.
Пирамида \( ABCT\) подобна пирамиде \( A_1B_1C_1T\) т.к. , из условия известно, что плоскости \(ABC\) и \(A_1B_1C_1\) параллельны.
Найдем коэффициент подобия .
Данные пирамиды подобны по сторонам. Согласно условия задачи точка \(A \) делит ребро \( A_1T\) на части $$ \frac{AT}{A_1A}=\frac{1}{3} => \frac{AT}{A_1A+AT}=\frac{1}{3+1} => \frac{AT}{A_1T}=\frac{1}{4}$$
Покажем, что все стороны и высота пирамид относятся с таким же коэффициентом. Для высоты \( h\) рассмотрим \( ΔA_1TO_1\) и \(ΔATO\) они подобны по 3-м углам, коэффициент подобия известен $$
\frac{AT}{A_1T} = \frac{OT}{O_1T} = \frac{h}{H}= \frac{1}{4}$$
Рассмотрим \( ΔA_1TB_1\) и \(ΔATB\) они также подобны по трем углам, соответственно $$ \frac{AT}{A_1T} = \frac{AB}{A_1B_1}= \frac{BT}{B_1T} = \frac{1}{4}$$ аналогично и для остальных ребер. Получили, что высота большой пирамиды равна \( H=4h\). Площадь основания \( S_{ABC} = \frac{1}{2}AB*AC*\sin (A)\). Выразим площадь основания большой пирамиды через площадь основания малой $$ S_{A_1B_1C_1} = \frac{1}{2}A_1B_1*A_1C_1*\sin (A) = $$$$ =\frac{1}{2}*4AB*4AC*\sin (A) = 4^2*S_{ABC}$$ получили, что отношение площадей оснований двух пирамид равно квадрату коэффициента подобия. Рассмотрим объемы двух пирамид и выразим объем большой пирамиды через объем маленькой. \(V_{ABCT} = \frac{1}{3}S_{ABC}*h\), а $$ V_{A_1B_1C_1T} = \frac{1}{3} S_{A_1B_1C_1}*H = $$$$ = \frac{1}{3} *4^2 * S_{ABC}*4h = 4^3 * V_{ABCT}$$ Получили ответ, из которого следует, что отношение объемов двух подобных тел равно кубу из коэффициента подобия.
Если в основании пирамиды будет лежать n-угольный многоугольник, то для нахождения его площади его нужно будет разбить на треугольники и найти их площадь. Полученные треугольники двух оснований будут подобны с известным коэффициентом, а площади оснований будут равны их сумме. А отсюда понятно, что площади любых оснований будут относиться друг к другу как отношение квадрата коэффициента подобия.
Получили, что коэффициент подобия двух пирамид равен \(4^3\), получим объем большей пирамиды $$ V_{A_1B_1C_1T} = 4^3*V_{ABC} $$ Согласно условия задачи известно, что объем усеченной пирамиды равен $$ V_{A_1B_1C_1ABC} = V_{A_1B_1C_1T} - V_{ABC} = 315 cm^3 => $$$$ 4^3*V_{ABC} - V_{ABC} = 315 cm^3 => $$$$ 63V_{ABC} = 315 cm^3 => V_{ABC} = 5 cm^3$$ получили объем маленькой пирамиды. Объем большой пирамиды можно получить либо путем умножения на коэффициент подобия $$V_{A_1B_1C_1T} = 4^3*V_{ABC} = 4^3*5 = 320 cm^3$$ или путем сложения объемов усеченной пирамиды и маленькой пирамиды $$V_{A_1B_1C_1T} = V_{A_1B_1C_1T} + V_{ABC} = 315 + 5 = 320 cm^3 $$
Ответ: объем пирамиды равен \(V_{A_1B_1C_1T} = 320 cm^3 \)



