
0 Голосов

|
 |
| Posted Март 7, 2013 by Вячеслав Моргун |
|
|
- Т.к. функция представляет собой рациональную дробь, то она определена и непрерывна всюду на бесконечной прямой, кроме точек \( x^2-1 \ne 0 => x \ne \pm 1\), в которой обращается в ноль знаменатель.
- Проанализируем функцию на предмет существования асимптот. Рассмотрим поведение функции в точках \( x = \pm 1\)
$$\lim_{x \to 1_{+0}} \frac{x^2+1}{x^2-1} = + \infty$$
$$\lim_{x \to 1_{-0}} \frac{x^2+1}{x^2-1} = - \infty $$
$$\lim_{x \to -1_{+0}} \frac{x^2+1}{x^2-1} = - \infty$$
$$\lim_{x \to -1_{-0}} \frac{x^2+1}{x^2-1} = + \infty$$получили, что график имеет две асимптоты \( x = \pm 1\), проверим на наличие наклонных асимптот
$$\lim_{x \to \pm \infty} \frac{f(x)}{x} = \lim_{x \to \pm \infty} \frac{x^2+1}{(x^2-1)x} = 0$$вывод, наклонных асимптот нет.
- Вычислим первую производную для нахождения области возрастания и убывания и критические точки.
$$y' = (\frac{x^2+1}{x^2-1}) = \frac{2x(x^2-1)-2x(x^2+1)}{(x^2-1)^2}= - \frac{4x}{(x^2-1)^2}$$
Приравняем производную к нулю и найдем критическую точку \( - \frac{4x}{(x^2-1)^2} = 0 => x = 0, y = -1\) Достаточным условием существования экстремума является - смена знака производной при переходе через критическую точку. Проанализируем знак производной справа и слева от критической точки
- \( (-1; 0)\) \( y'(- \frac{1}{2}) = - \frac{4x}{(x^2-1)^2} = - \frac{4*(-\frac{1}{2})}{(\frac{1}{2}^2-1)^2} > 0 \) функция возрастает
- \( (0; 1)\) \( y'(\frac{1}{2}) = - \frac{4x}{(x^2-1)^2} = - \frac{4*\frac{1}{2}}{(\frac{1}{2}^2-1)^2} < 0 \) функция убывает
Вывод точка \( x=0; y=-1\) - точка максимума
- Для нахождения областей выпуклости найдем вторую производную
$$y'' = -( \frac{4x}{(x^2-1)^2}) = - \frac{4(x^2-1)^2- 4x*2(x^2-1)2x}{(x^2-1)^4}=\frac{3x^4-2x^2-1}{(x^2-1)^4} = \frac{(x^2-1)(x^2+\frac{1}{3})}{(x^2-1)^4} = 0$$получили \( x = \pm 1\). На основании данных второй производной и ОДЗ рассмотрим интервалы и значение второй производной на них
- \( -\infty; -1\) \( y''(-2) = \frac{(x^2-1)(x^2+\frac{1}{3})}{(x^2-1)^4} > 0\) выпуклая вниз
- \( -1; 1\) \( y''(0) = \frac{(x^2-1)(x^2+\frac{1}{3})}{(x^2-1)^4} < 0\) выпуклая вверх
- \( 1; +\infty\) \( y''(2) = \frac{(x^2-1)(x^2+\frac{1}{3})}{(x^2-1)^4} > 0\) выпуклая вниз
- Найдем точки пересечения с осью \( x\)
$$\frac{x^2+1}{x^2-1} = 0 $$точек пересечения нет.
Найдем точки пересечения с осью \( y\)
$$y(0) = \frac{x^2+1}{x^2-1} = \frac{0^2+1}{0^2-1} = -1 $$ \( x = 0; y = -1\) точка пересечения с осью \( y\)
- Строим график
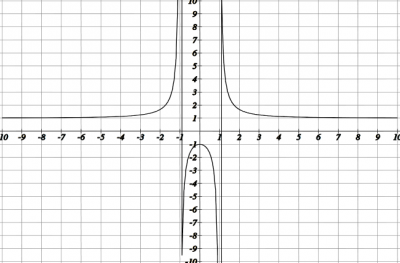
|
|



