В задаче говорится, что есть два треугольника равнобедренных, у которых углы при основании равны. Вывод эти треугольники подобны по трем углам, т.е. свойства у них одинаковые, а значит биссектриса угла второго треугольника также делит высоту в пропорции \( \frac{5}{3}\). Рассмотри рисунок
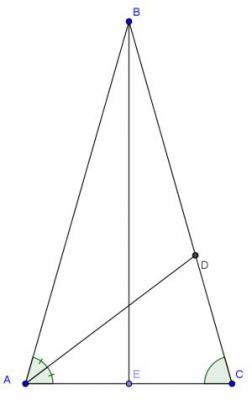
Вспомним свойство биссектрисы треугольника - биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам. Применим это свойство к треугольнику ΔABE
$$\frac{BO}{OE}=\frac{5}{3}=\frac{AE}{AB} \, (1)$$в то же время высота, опущенная из вершины равнобедренного треугольника совпадает с медианой, т.е. точка \( E\) делит сторону пополам. Обозначим \( AB = BC = x\), \( AC = y \), тогда (1) примет вид $$\frac{\frac{1}{2}y}{x} = \frac{5}{3}$$ Из условия известно, что $$ P = 2x + y = 48 , (2) $$ Составим систему уравнений из (1) и (2)
$$\begin{cases}\frac{\frac{1}{2}y}{x} = \frac{5}{3} \\ 2x + y = 48 \end{cases} =>\begin{cases}\frac{y}{2x} = \frac{5}{3} \\ 2x = 48 -y \end{cases} =>$$
$$\begin{cases}\frac{y}{48 - y} = \frac{5}{3} \\ 2x = 48 -y \end{cases} =>\begin{cases} 3y = 5*(48 - y) \\ 2x = 48 -y \end{cases} =>$$
$$\begin{cases} 8y = 5*48 \\ 2x = 48 -y \end{cases} =>\begin{cases} y = 30 \\ x = 9 \end{cases}$$
Ответ: стороны треугольника равны : катеты по 9 см, основание 30 см.



