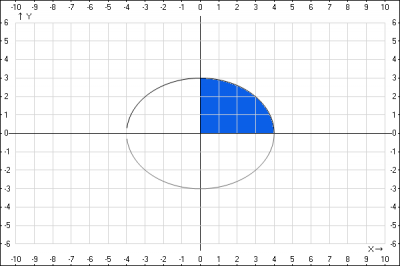
Решение: рассмотрим рисунок. Из рисунка видно, что искомая фигура ограниченная линиями сверху \( \frac{x^{2}}{16}+\frac{y^{2}}{9}=1 \) слева \(y=0\) снизу \(x=0\), т.е нам нужно найти площадь эллипса в первой четверти. Длина большой полуоси равна \(a^2 = 16 => a=4\). Преобразуем уравнение эллипса с учетом того,что в первой четверти \(x > 0, \quad y > 0\), получаем $$ \frac{x^{2}}{16}+\frac{y^{2}}{9}=1 => y = 3\sqrt{1- \frac{x^2}{16}}$$ получили явно выраженную функцию \(y = f(x)\). Находим площадь фигуры $$S = \int_0^43\sqrt{1- \frac{x^2}{16}}dx = \quad (1)$$
1. Найдем неопределенный интеграл \( \int \sqrt{1- \frac{x^2}{16}}dx \)Применим формула интегрирования по частям \( \int udv = uv - \int vdu\). Введем обозначения \(dv = dx => v = x\), а \(u = \sqrt{1- \frac{x^2}{16}} => du = -\frac{x}{16\sqrt{1- \frac{x^2}{16}}}dx \), подставляем $$ \int \sqrt{1- \frac{x^2}{16}}dx = x \sqrt{1- \frac{x^2}{16}} + \int x* \frac{x}{16\sqrt{1- \frac{x^2}{16}}}dx =$$
выделим целую часть в дроби интеграла $$ = x \sqrt{1- \frac{x^2}{16}} - \int \frac{1 - \frac{x^2}{16} - 1}{\sqrt{1- \frac{x^2}{16}}}dx = x \sqrt{1- \frac{x^2}{16}} - \int \sqrt{1- \frac{x^2}{16}}dx + \int \frac{1}{\sqrt{1- \frac{x^2}{16}}}dx = $$ применим формулу табличного интеграла арксинуса \( \int \frac{1}{ \sqrt{1-(ax)^2}} = \frac{1}{a}\arcsin(ax)\), получаем $$ \int \sqrt{1- \frac{x^2}{16}}dx = x \sqrt{1- \frac{x^2}{16}} - \int \sqrt{1- \frac{x^2}{16}}dx + 4\arcsin(\frac{x}{4}) =>$$ справа и слева получили равные интегралы, перенесем их в левую часть равенства $$ 2 \int \sqrt{1- \frac{x^2}{16}}dx = x \sqrt{1- \frac{x^2}{16}} + 4\arcsin(\frac{x}{4}) => $$$$ \int \sqrt{1- \frac{x^2}{16}}dx = \frac{1}{2}x \sqrt{1- \frac{x^2}{16}} + 2\arcsin(\frac{x}{4})$$
2. подставляем результата в (1) $$ S = 3\int_0^4\sqrt{1- \frac{x^2}{16}}dx = 3(\frac{1}{2}x \sqrt{1- \frac{x^2}{16}} + 2\arcsin(\frac{x}{4}))|_0^4 = $$ применим формулу Ньютона - Лейбница \(\int_a^bf(x)dx = F(b) - F(a)\), получаем $$ = 3(\frac{1}{2}*4 \sqrt{1- \frac{4^2}{16}} + 2\arcsin(\frac{4}{4}) - \frac{1}{2}0 \sqrt{1- \frac{0^2}{16}} 0 2\arcsin(\frac{0}{4})) =3\pi $$
Ответ: площадь фигуры, ограниченная заданными линиями сверху \( \frac{x^{2}}{16}+\frac{y^{2}}{9}=1 \) слева \(y=0\) снизу \(x=0\) равна \(S = 3\pi \)