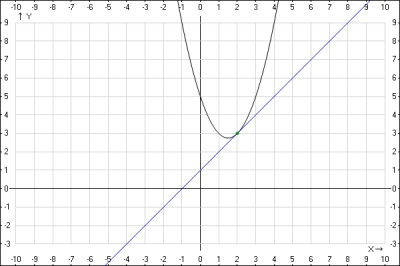
Решение: найдем уравнение касательной прямой к параболе в заданной точке. Воспользуемся уравнением касательной к кривой в точке $$ f(x) = f(x_0) + f'(x_0)(x-x_0)$$
1. найдем значение функции в точке \(P(2;3)\), \(f(x_0) = f(2) = 3\).
2. найдем значение первой производной в этой точке \(f'(x) = (x^2-3x+5)' = 2x-3 => f'(2) = 2*2-3=1\)
3. подставляем результаты в формулу касательной $$ y = 3 + 1(x-2) => $$ получили уравнение касательной в точке \(P(2;3)\) $$ y = x + 1$$
4. угловой коэффициент прямой - тангенс угла наклона прямой к оси \(Ox\), т.е. $$k = tg(\alpha) = 1 => \alpha = arctg(1) =\frac{ \pi}{4}$$
Ответ:
1. уравнение касательной к точке \( y = x + 1\)
2. угол наклона касательной с оси Ox равен \( \alpha = \frac{ \pi}{4} \)