Визначте площу фігури, яка обмежена лініями: $y=2^x$ $y=3-x$ $x=0$

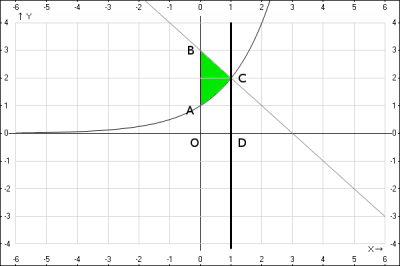
Решение: из рисунка видно, что искомая фигура ограничена сверху линией $y = 3-x$, а снизу $y = 2^x$. Найдем точку пересечения прямых

$$\begin{cases}y = 3-x\\ y = 2^x\end{cases} => \begin{cases}2^x = 2-x \\ y = 2^x\end{cases}$$ $$\begin{cases}x = 1 \\ y = 2 \end{cases}$$ Из геометрического смысла определенного интеграла следует, что $S_{OBCD} = \int_0^1(3-x)dx$, а $S_{OACD} = \int_0^12^xdx$. А искомая площадь $S_{ABC} = S_{OBCD} - S_{OACD}$, т.е. искомую площадь можно представить в виде $S = \int (f(x)-g(x))dx$, где $f(x)$ - линия сверху, а $g(x)$  - линия снизу . Подставляем интегралы в формулу площади  $$S_{ABC} = \int_0^1 (3-x - 2^x)dx = (3x-\frac{x^2}{2} - \frac{2^x}{\ln(2)})|_0^1 =$$ $$= 3-\frac{1}{2} - \frac{2^1}{\ln(2)} - 3*0 + \frac{0}{2} +  \frac{2^0}{\ln(2)} =$$ $$= \frac{5}{2} - \frac{2^1}{\ln(2)} + \frac{1}{\ln(2)} = \frac{5}{2} - \frac{1}{\ln(2)}$$
Ответ: площадь фигуры, ограниченная заданными линиями равна $S_{ABC} =  \frac{5}{2} - \frac{1}{\ln(2)}$