Решение: при вращении криволинейной трапеции вокруг оси Ox, которая ограничена сверху прямой \( y = x+1\), а справа и слева прямыми \(x=0\) и \(x=2\) и снизу прямой \(y =1\), образуется тело - обрезанный конус, у которого вырезан в центре цилиндр.
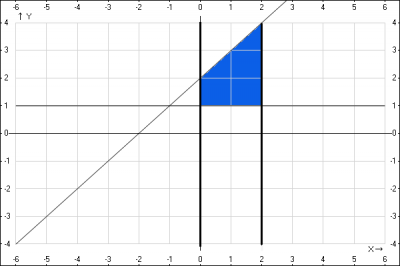
1. Найдем объем обрезанного конуса.
Рассчитаем объем обрезанного конуса по формуле $$V_x = \pi \int_a^b y^2dx$$ где \(a = 0\), \(b=2\), \(y^2 = (x+1)^2\). Подставляем данные в формулу $$V_x = \pi \int_0^2 (x+1)^2dx = \pi \frac{1}{2+1}(x+1)^{2+1}|_0^2 $$$$ = \frac{\pi}{3}(x+1)^3|_0^2 = \frac{\pi}{3}(2+1)^3 - \frac{\pi}{3}(0+1)^3 = \frac{26\pi}{3}$$
2. Найдем объем цилиндра.
Объем цилиндра рассчитывается по формуле $$V_{ц} = S_{осн}h$$ где площадь основания равна \( S_{осн} = \pi r^2 = \pi 1^2 = \pi\), а высота, опущенная на основание \(h = 2\). Подставляем в формулу объема $$V_{ц} = 2\pi$$
3. Находим объем фигуры вращения.
Объем фигуры вращения равен разности объемов обрезанного конуса и цилиндра
$$V = V_x - V_{ц} = \frac{26\pi}{3} - 2\pi = \frac{20\pi}{3}$$
Ответ: объем фигуры вращения равен \(V = \frac{20\pi}{3}\)





