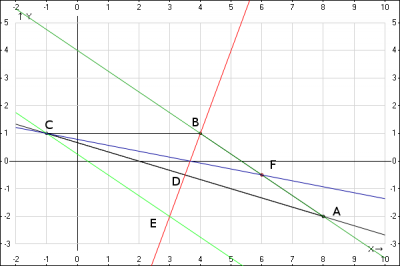
Даны координаты вершин треугольника: А (8;-2); В(4;1); С(-1;1)
Найти:
в) уравнение высоты треугольника \(ΔАВС\), которая проходит через вершину \(B\)
Уравнение высоты треугольника, проходящую через вершину B.
Схема нахождения: высота из вершины \(B\) (обозначим ее \(BD\)) перпендикулярна прямой \(AC\) и их угловые коэффициенты связаны соотношением \(k_1*k_2=-1\) поэтому найдем уравнение прямой \(AC\), получим угловой коэффициент высоты.
Решение: уравнение прямой \(AC\) будем находим по формуле уравнения прямой, проходящей через две заданные точки \(A\) и \(C\) : $$ \frac{x-x_A}{x_C-x_A}=\frac{y-y_A}{y_C-y_A}$$ подставляем координаты точек $$ \frac{x-8}{-1-8}=\frac{y+2}{1+2} => y = -\frac{1}{3}x + \frac{2}{3}$$ Находим угловой коэффициент $$k_{AC}*k_{BD}=-1 => k_{BD} = 3$$ Получили угловой коэффициент \(k_{BD} = 3\). Подставляем в уравнение прямой \(y - y_0 = k(x-x_0)\) - уравнение проходящей через заданную точку \(B\) в заданном направлении \(k_{BD}\) , получаем уравнение искомой высоты \(BD\) $$y - 1 = 3(x-4) => y = 3x - 11$$
Ответ: уравнение высоты \( y = 3x - 11 \)
с) уравнение прямой, которая проходит через точку \(C\), параллельно прямой \(AB\)
Схема нахождения: уравнение прямой \(CE\) (обозначим ее \(CE\)) и уравнение параллельной ей прямой \(AB\) имеют равные угловые коэффициенты \(k_{AB} =k_{CE}\) поэтому найдем уравнение прямой \(AB\), получим угловой коэффициент, а затем уравнение прямой \(CE\) будем находим по формуле уравнения прямой, проходящей через заданную точку в заданном направлении \(y - y_0 = k(x-x_0)\)
Решение: находим уравнение прямой \(AB\) по формуле уравнения прямой, проходящей через две заданные точки \(A\) и \(B\) : $$ \frac{x-x_A}{x_B-x_A}=\frac{y-y_A}{y_B-y_A}$$ подставляем координаты точек $$ \frac{x-8}{4-8}=\frac{y+2}{1+2} => y = -\frac{3}{4}x + 4$$ Находим угловой коэффициент $$k_{AB} = k_{CE} =-\frac{3}{4} $$ Получили угловой коэффициент \(k_{CE} = -\frac{3}{4}\). Подставляем в уравнение прямой \(y - y_0 = k(x-x_0)\), получаем уравнение прямой \(CE\) $$y - 1 = -\frac{3}{4}(x+1) => y = -\frac{3}{4}x + \frac{1}{4}$$
Ответ: уравнение прямой \( y = -\frac{3}{4}x + \frac{1}{4}\)
д) уравнение медианы треугольника \(ΔАВС\), которая проходит через вершину \(C\)
Для нахождения медианы (обозначим ее \(CF\)) есть координата одной точки (С), а координаты второй точки прямой \(F\) найдем как координаты середины отрезка \(BC\) по формуле \( F(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2})\) => \( F(\frac{8+4}{2};\frac{-2+1}{2}) \) => \( F(6; -\frac{1}{2}) \)
Решение: находим уравнение прямой \(CF\) по формуле уравнения прямой, проходящей через две заданные точки \(C\) и \(F\) : $$ \frac{x-x_C}{x_F-x_C}=\frac{y-y_C}{y_F-y_C}$$ подставляем координаты точек $$\frac{x+1}{6+1}=\frac{y-1}{-\frac{1}{2}-1} => y = -\frac{3}{14}x + \frac{11}{14}$$
Ответ: уравнение медианы \( y = -\frac{3}{14}x + \frac{11}{14}\)
е) длину высоты треугольника \(ΔАВС\), которая проходит через вершину \(C\)
Длина высоты - расстояние от точки до прямой, которое рассчитывается по формуле \(d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \), где \((x_0;y_0)\) - координаты точки, а
\(Ax_0+By_0+C =0\) - общее уравнение прямой, расстояние между которыми ищется.
Решение: приводим уравнение прямой \(AB\) к общему виду \(y = -\frac{3}{4}x + 4 => 3x +4y - 16 =0\), где \(A =3\), \(B = 4\) подставляем в формулу $$d = \frac{|3(-1) +4*1 - 16|}{\sqrt{3^2+4^2}} = 3$$
Ответ: длина высоты равна \(d = 3\)