Построим фигуру, площадь которой необходимо найти (см. рис 1).
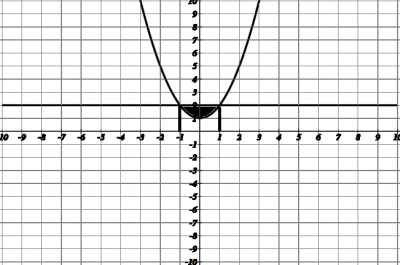
(рис. 1)
Это закрашенная фигура. Геометрический смысл интеграла - площадь фигуры, ограниченная сверху кривой, снизу осью \( x \) на заданном отрезке. Найдем отрезок - отрезок между точками пересечения кривых. Найдем эти точки. В точке пересечения кривых \( x, y\) у них равны, поэтому приравняем уравнения и найдем \( x \) $$\begin{cases}y-2 = 0\\ y = 1 + x^2 \end{cases}=>\begin{cases}y = 2\\ 2 = 1 + x^2 \end{cases}=>\begin{cases}y = 2\\ x = \pm 1 \end{cases}$$т.е. мы получили нижнюю и верхняя границы интеграла. Фигура, ограниченной прямой \( y -2 =0\) на отрезке \( [-1;1]\) - это прямоугольник (ограничен прямой, осью \( x \) и перпендикулярами из точек пересечения), его площадь равна \( S_1 = a*b\), где \(a =2, b=2\), \( S_1 = 4 \). Фигура, ограниченная кривой \( y = 1 + x^2 \) - сверху ограничена кривой, снизу осью \( x \), по бокам перпендикулярами из точек пересечения, по определению - определенный интеграл от этой функции на заданном отрезке, получаем $$S_2 = \int_{-1}^{1}(1+x^2) dx = x + \frac{1}{3}x^3 |_{-1}^{1} = 1 + \frac{1}{3} - (-1-\frac{1}{3}) = 2\frac{2}{3}$$площадь закрашенной фигуры - разность двух площадей $$S = S_1 - S_2 = 4 - 2\frac{2}{3} = 1\frac{1}{3}$$
Ответ: площадь фигуры равна \(S = 1\frac{1}{3} \)



