Рассмотрим по отдельности движение шайбы вниз и вверх и запишем уравнения движения.
1. Движение вниз по наклонной плоскости вниз.
На шайбу действуют следующие силы (смотрим рисунок )
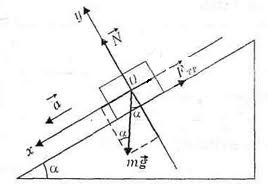
\(m\vec{g}\) - сила тяжести, приложенная к центру масс,
\(N\) - сила нормальной реакции наклонной плоскости, эта сила перпендикулярна плоскости,
\(F_{тр}\) - сила трения скольжения, параллельная наклонной плоскости и направлена противоположно скорости (направлению) движения шайбы.
Ось Ох направлена вдоль плоскости, в сторону движения шайбы.
Составим уравнение движения в векторной форме $$m\vec{g}+\vec{F_{тр}}+\vec{N} = m\vec{a_{вниз}}$$Найдем проекции всех сил на ось Ох.
- Сила нормальной реакции опоры направлена перпендикулярно ось Ох, поэтому ее проекция на ось Ох равна 0 \(N_x=0\).
- Сила трения \(\vec{F_{тр}}\) параллельна оси Ох, но ее направление противоположно направлению оси Ох, поэтому проекция силы \(\vec{F_{тр}}\) на ось Ох равна \(-F_{тр}\).
- Проекция силы тяжести \(m\vec{g}\) на ось Ох равна \(mg\sin \alpha\)
Зная проекции всех сил на эту ось, в составить со вторым законом Ньютона получаем $$mg\sin\alpha - F_{тр} = ma_{вниз}$$ Т.к. сила трения равна $$F_{тр} = \mu N$$ получаем $$mg\sin\alpha - \mu N = ma \quad (1)$$Найдем проекции всех сил на ось Оу.
- ускорение вдоль оси Оу равно нулю \(a=0\)
поэтому проекции всех остальных сил на ось Оу будут иметь следующий вид $$mg\cos\alpha - N =0 => N = mg\cos\alpha$$
Т.е. проекция на ось Оу нужна была, чтобы найти уравнение силы нормальной реакции опоры, которое подставим в (1), получаем $$mg\sin\alpha - \mu mg\cos\alpha = ma_{вниз} =>$$$$g\sin\alpha - \mu g\cos\alpha = a_{вниз} $$
Получили уравнение с двумя неизвестными \(a_{вниз}\) и \(\mu\), нам нужно второе уравнение для составления системы уравнений. Второе уравнение мы получим из второй части задачи - движение шайбы вверх.
2. Движение вниз по наклонной плоскости вверх.
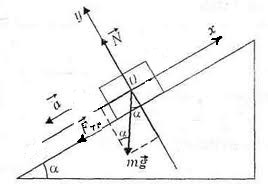
Составим уравнение движения в векторной форме $$m\vec{g}+\vec{F_{тр}}+\vec{N} = m\vec{a_{вверх}}$$
Найдем проекции всех сил на ось Ох по аналогии с п.1.
В данном случае шайба останавливается под действием силы тяжести и силы трения, проекции, которых вдоль оси Ох направлены в сторону противоположную движению. Зная проекции всех сил на эту ось, в соответствии со вторым законом Ньютона получаем $$-mg\sin\alpha - \mu mg\cos\alpha = ma_{вверх}=>-g\sin\alpha - \mu g\cos\alpha = a_{вверх}$$ В задаче у нас есть еще одно условие - шайба остановилась в два раза быстрее при подъеме, чем при спуске. Рассмотрим формулу ускорения $$a=\frac{Δv}{Δt}$$При движении вниз скорость менялась от 0 до \(v\), при движении вверх от \(v\) до 0, т.е. \(Δv\) постоянная, а время при движении вверх в 2 раза меньше, т.е. \(a_{вверх}=\frac{Δv}{\frac{1}{2}Δt}=2*\frac{Δv}{Δt}=2a_{вниз}=2a\)
Теперь можно составить систему уравнений:
$$\begin{cases}g\sin\alpha - \mu g\cos\alpha = a\\-g\sin\alpha - \mu g\cos\alpha = 2a\end{cases}=> \begin{cases}2g\sin\alpha - 2\mu g\cos\alpha = -g\sin\alpha - \mu g\cos\alpha\\-g\sin\alpha - \mu g\cos\alpha = 2a\end{cases}=> $$$$ \begin{cases}\mu g\cos\alpha=3g\sin\alpha\\-g\sin\alpha - \mu g\cos\alpha = 2a\end{cases}=>\begin{cases}\mu=3tg \alpha\\-g\sin\alpha - \mu g\cos\alpha = 2a\end{cases}=> $$$$ \begin{cases}\mu=3\\-g\sin\alpha - \mu g\cos\alpha = 2a\end{cases}$$Мы учли \(tg \alpha = tg 45^0 =1\)
Ответ: коэффициент трения равен \(\mu = 3\)



