Рішення: розглянемо малюнок
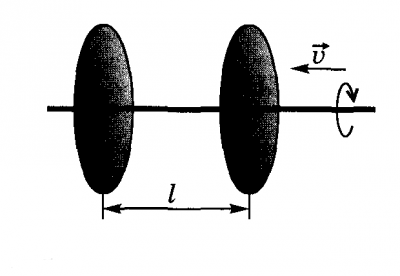
Будемо вважати, що після пробиття першого диска швидкість кулі і напрямок руху не змінилися.
Куля летить рівномірно і прямолінійно. Швидкість рівномірного прямолінійного руху дорівнює $$ V = \frac{S}{t} \quad (1) $$ де \(S \) - відстань, пройдену кулею. В даному випадку відстань дорівнює відстані між дисками \(S = L = 0.5 м \).
Потрібно знайти час.
Шукаємо час : відомо, що диски обертаються з частотою \(n = 1600 об / хв \), тобто один повний оберт диск зробить за \( T = \frac{60}{n} = \frac{60}{1600} сек \) - період обертання в секундах. Відомо, що після того, як був пробитий перший диск, другий встиг зміститися на \(12 ^ 0 \) поки до нього летіла куля, тобто куля летіла \( \frac{12 ^ 0} {360 ^ 0} \) - частку періоду, тобто час польоту кулі \( t = \frac{12^0}{360^0}*T = \frac{12^0}{360^0} \frac{60}{1600} = \frac{1 }{800} \).
Підставляємо час і відстань в (1), отримуємо $$ V = \frac{S}{t} = \frac{0.5}{ \frac{1}{ 800}} = 400 м / сек $$
Відповідь : швидкість кулі дорівнює \( V = 400м / сек \)



