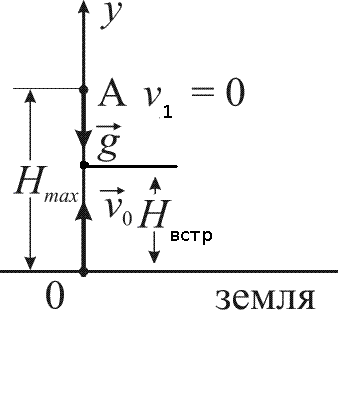
Задание: тело брошено вертикально вверх с начальной скоростью \(V_0 = 4м/с\). Когда оно достигло верхней точки полета с того же начального пункта с той же начальной скоростью \(V_0\) вертикально вверх кинуто другое тело. На какой высоте \(h\) от начального пункта встретятся тела? Сопротивлением воздуха пренебречь.
Решение: определим план решения. Первое тело, подброшенное вверх достигло наивысшей точки (высота \(H\)) и под действием силы тяжести начинает падать вниз с ускорением свободного падения \(g\), при этом начальная скорость его при падении равна \(V_1=0\).
1. Найдем высоту, на которую поднимется первое тело \(H_1\). Запишем уравнение скорости в векторной форме \( \vec{v}= \vec{v_0} + \vec{g}t\). Вектора скорости и ускорения противонаправленны, поэтому проекция вектора скорости на вертикальную ось будет иметь вид $$v = v_0 - gt =>$$ т.к. в наивысшей точке \(A\) скорость \(v=0\), то получим время подъема $$ t = \frac{v_0}{g}$$ тогда высоту подъема найдем по формуле $$ H = v_0t -\frac{gt^2}{2} = $$ подставляем найденное время $$ H = v_0* \frac{v_0}{g} - \frac{gv_0^2}{2g^2} = \frac{v_0^2}{g} - \frac{v_0^2}{2g} = \frac{v_0^2}{2g}$$
2. Найдем высоту встречи. Первое тело движется вниз с ускорением и начальной скоростью \(v_1=0\) уравнение движения которого \(H_{встр.} = H - \frac{gt^2}{2}\), а второе вертикально вверх \(H_{встр.} = v_0t - \frac{gt^2}{2}\). Приравняем два эти уравнения, т.к. высоты у тел при встрече равны $$H - \frac{gt^2}{2} = v_0t - \frac{gt^2}{2} => H = v_0t = > t = \frac{H}{v_0}$$ подставляем формулу высоты \(H\) $$ t = \frac{v_0^2}{2g*v_0} = \frac{v_0}{2g}$$Получили время, через которое тела встретятся. Подставим время в уравнение высоты и найдем ее $$H_{встр.} = H - \frac{gt^2}{2} = \frac{v_0^2}{2g} - \frac{gv_0^2}{2*4g^2} = \frac{3v_0^2}{8g}$$ Подставляем данные задачи $$H_{встр.} = \frac{3}{8}\frac{(4m/c)^2}{10m/c^2} = \frac{3}{8}\frac{16}{10}m = 0.6 m$$
Ответ: тела встретятся на высоте 0.6 м.