Найдем площадь фигуры, ограниченную кривыми \( y=x^2; \quad y=-x^2+ 2\).
1. Сделаем чертеж, на чертеже обозначим фигуру, площадь которой требуется найти.
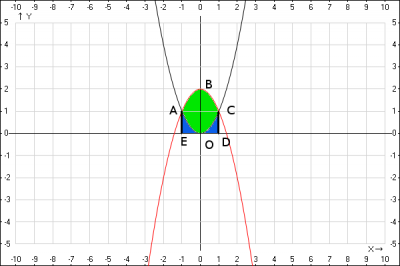
2. Найдем площадь фигуры \(ABCO\).
Фигура, ограниченная заданными кривыми - \(ABCO\). Данная фигура симметрична относительно оси Oy, поэтому ее площадь равна $$S_{ABCO} = 2S_{OBC} \quad (1)$$
Из рисунка видно, что $$S_{OBC} = S_{OBCD} - S_{OCD} \quad (2)$$
Найдем площадь фигуры \(OBCD\). Для нахождения площади этой фигуры воспользуемся геометрическим смыслом определенного интеграла - определенный интеграл равен площади фигуры, ограниченной графиком функции \(y=-x^2+ 2\), осью Ox и перпендикулярами на эту ось \(x = x_B\) и \(x =x_C\). Найдем координаты точек \(B\) и \(C\)
Точка \(B\) - точка пересечения параболы \(y=-x^2+ 2\) с осью Oy, т.е. \(x_B=0\)
Точка \(C\) - точка пересечения парабол \( y=x^2; \quad y=-x^2+ 2 \). Составим систему уравнений и учтем, что мы рассматриваем фигуру только справа от оси Oy, т.е. при \( x \geq 0\) из-за соображений симметрии $$ \begin{cases}y=x^2 \\ y=-x^2+ 2\\ x \geq 0 \end{cases} => \begin{cases}-x^2+ 2 = x^2 \\ y= -x^2+ 2 \\ x \geq 0 \end{cases} =>$$$$ \begin{cases} x= \pm 1 \\ y= -x^2+ 2 \\ x \geq 0 \end{cases} => \begin{cases} x= 1 \\ y= 1 \\ x \geq 0 \end{cases}$$ Найдем площадь фигуры \(OBCD\)
$$S_{OBCD} = \int_0^1(-x^2+ 2)dx = -\frac{1}{3}x^3 + 2x|_0^1 = -\frac{1}{3} + 2 = \frac{5}{3}$$
Найдем площадь фигуры \(OCD\)
$$S_{OCD} = \int_0^1x^2dx = \frac{1}{3}x^3|_0^1 = \frac{1}{3}$$
Полученные результаты подставим в (2)
$$S_{OBC} = S_{OBCD} - S_{OCD} => S_{OBC} = \frac{5}{3} - \frac{1}{3} = \frac{4}{3}$$ тогда площадь искомой фигуры \(ABCO\), согласно формулы (2), равна $$ S_{ABCO} = 2S_{OBC} => S_{ABCO} = 2*\frac{4}{3} = \frac{8}{3}$$
Ответ: площадь фигуры, ограниченную кривыми \( y=x^2; \quad y=-x^2+ 2\) равна \( S_{ABCO} = \frac{8}{3} \).



