–∞) –Э–∞–є–і–µ–Љ –Ј–љ–∞—З–µ–љ–Є–µ –њ–Њ—Б—В–Њ—П–љ–љ–Њ–є \(C\) —Д—Г–љ–Ї—Ж–Є–Є –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П \(f(x)\). –Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —Д—Г–љ–Ї—Ж–Є—П \(f(x)\) –±—Л–ї–∞ –њ–ї–Њ—В–љ–Њ—Б—В—М—О —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л \(x\) –Ї–Њ–љ—Б—В–∞–љ—В–∞ \(C\) –і–Њ–ї–ґ–љ–∞ –±—Л—В—М \(C \geq 0\). –Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Ј–љ–∞—З–µ–љ–Є—П –Ї–Њ–љ—Б—В–∞–љ—В—Л –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Г—Б–ї–Њ–≤–Є–µ–Љ \( \int_{ \alpha}^{ \beta} f(x) = 1\), –њ–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –і–∞–љ–љ—Л–µ –Ј–∞–і–∞—З–Є: $$ \int_{0}^{ \sqrt{3}}{ \frac{C}{(1+x^2)}} =1 => C *arctg(x)|_{0}^{ \sqrt{3}} = 1 =>$$$$C \frac{ \pi}{3} = 1 => C = \frac{3}{ \pi}$$–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤ —Д–Њ—А–Љ—Г–ї—Г –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –љ–∞ –Є–љ—В–µ—А–≤–∞–ї–µ \((0; \sqrt{3})\), –њ–Њ–ї—Г—З–∞–µ–Љ \(f(x) = \frac{3}{\pi(1+x^2)} \)
–Ю—В–≤–µ—В: –њ–Њ—Б—В–Њ—П–љ–љ–∞—П \(C = \frac{3}{ \pi}\), –∞ —Д—Г–љ–Ї—Ж–Є—П —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –љ–∞ –Є–љ—В–µ—А–≤–∞–ї–µ \((0; \sqrt{3})\) —А–∞–≤–љ–∞ \(f(x) = \frac{3}{\pi(1+x^2)} \)
–±) –Э–∞–є–і–µ–Љ —Д—Г–љ–Ї—Ж–Є—О —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П \(F(x)\). –Ф–ї—П —А–µ—И–µ–љ–Є—П –Ј–∞–і–∞—З–Є –≤–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П —Д–Њ—А–Љ—Г–ї–Њ–є \( \int_{-\infty}^{x}f(t)dt = F(x)\). –Э–∞–є–і–µ–Љ —Д—Г–љ–Ї—Ж–Є—О —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –љ–∞ –Є–љ—В–µ—А–≤–∞–ї–∞—Е
\( x \leq 0 \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{x}0dt = 0$$
\( 0 < x \leq \sqrt{3} \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{0}f(t)dt + \int_{0}^{ x}f(t)dt = $$$$ = \int_{-\infty}^{0}0dt + \int_{0}^{ x}\frac{3}{\pi(1+t^2)}dt = 0 + \frac{3}{ \pi} arctg(x) = \frac{3}{ \pi} arctg(x) $$
\( \sqrt{3} < x \) $$ F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{0}f(t)dt + \int_{0}^{ \sqrt{3}}f(t)dt + \int_{ \sqrt{3}}^{ x}f(t)dt = $$$$ = \int_{-\infty}^{0}0dt + \int_{0}^{ \sqrt{3}}\frac{3}{\pi(1+t^2)}dt + \int_{ \sqrt{3}}^{x}0dt = $$$$ = 0 + \frac{3}{ \pi} arctg( \sqrt{3}) + 0 = $$$$ = 0 + \frac{3}{ \pi} \frac{ \pi}{3} +0 = 1$$
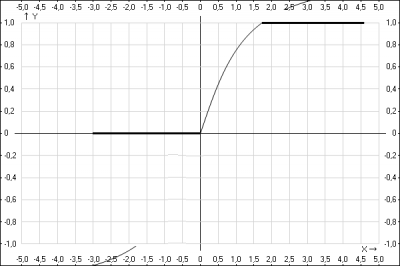
–Ю—В–≤–µ—В: —Д—Г–љ–Ї—Ж–Є—П —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –Є–Љ–µ–µ—В –≤–Є–і: $$ F(x) = \begin{cases}0 & x \leq 0\\ \frac{3}{ \pi} arctg(x) & 0 < x \leq \sqrt{3}\\ \\ 1 & \sqrt{3} < x \end{cases} $$
–≤) –Э–∞–є–і–µ–Љ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ–ґ–Є–і–∞–љ–Є–µ \(M(x)\)
–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–ґ–Є–і–∞–љ–Є–µ–Љ –љ–µ–њ—А–µ—А—Л–≤–љ–Њ–є —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л \(X\), –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –Ї–Њ—В–Њ—А–Њ–є –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—В –Њ—В—А–µ–Ј–Ї—Г \([a;b]\) –љ–∞—Е–Њ–і–Є—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$M(x) = \int_{a}^{b}xf(x)dx$$–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ–ґ–Є–і–∞–љ–Є–µ —А–∞–≤–љ–Њ $$M(x) = \int_{0}^{\sqrt{3}}\frac{3x}{\pi(1+x^2)}dx = $$ –≤–≤–µ–і–µ–Љ –Ј–∞–Љ–µ–љ—Г \(t^2 = 1+x^2 => 2tdt = 2xdx => tdt = xdx\), –њ–Њ–ї—Г—З–∞–µ–Љ \( \int \frac{3t}{\pi t^2}dt = \int \frac{3}{ \pi t}dt = \frac{3}{ \pi}\ln(t) = \) –њ—А–Є–Љ–µ–љ—П–µ–Љ –Њ–±—А–∞—В–љ—Г—О –Ј–∞–Љ–µ–љ—Г \( = \frac{3}{ \pi} \ln(\sqrt{1+x^2})\). –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤ —Д–Њ—А–Љ—Г–ї—Г –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–ґ–Є–і–∞–љ–Є—П $$ = \frac{3}{ \pi} \ln(\sqrt{1+x^2})|_{0}^{\sqrt{3}} = \frac{3}{ \pi} \ln(\sqrt{1+( \sqrt{3})^2}) - \frac{3}{ \pi} \ln(\sqrt{1+0^2}) =$$$$ = \frac{3}{ \pi} \ln(\sqrt{1+3}) = \frac{3}{ \pi} \ln(\sqrt{4}) = \frac{3}{ \pi}\ln(2) \approx 0,662$$
–Ю—В–≤–µ—В: –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ–ґ–Є–і–∞–љ–Є–µ —А–∞–≤–љ–Њ \(M(x) = 0,662\)
–≥) –Э–∞–є–і–µ–Љ –і–Є—Б–њ–µ—А—Б–Є—О \(D(x)\)
–Ф–Є—Б–њ–µ—А—Б–Є—О –љ–µ–њ—А–µ—А—Л–≤–љ–Њ–є —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л –±—Г–і–µ–Љ –Є—Б–Ї–∞—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ \(D(x) = \int_{ \alpha}^{ \beta}(x - M(x))^2f(x)dx\). –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –Є—Б—Е–Њ–і–љ—Л–µ –і–∞–љ–љ—Л–µ –≤ —Д–Њ—А–Љ—Г–ї—Г –і–Є—Б–њ–µ—А—Б–Є–Є$$D(x) = \int_{ 0}^{ \sqrt{3}}(x - \frac{3}{ \pi}\ln(2))^2\frac{3}{\pi(1+x^2)}dx = $$$$ =\frac{3}{\pi}(\int_{ 0}^{ \sqrt{3}}\frac{x^2}{1+x^2}dx - 2\int_{ 0}^{ \sqrt{3}}\frac{x \frac{3}{ \pi}\ln(2)}{1+x^2}dx + \int_{ 0}^{ \sqrt{3}}(\frac{3}{ \pi}\ln(2))^2\frac{1}{1+x^2}dx) =$$$$ = \frac{3}{\pi}(x - arctg(x)|_{0}^{\sqrt{3}} - \frac{6}{ \pi}\ln(2) \ln(\sqrt{1+x^2})|_{0}^{\sqrt{3}} + (\frac{3}{ \pi}\ln(2))^2arctg(x)|_{0}^{\sqrt{3}}) = $$$$ = \frac{3}{\pi}( \sqrt{3} - arctg( \sqrt{3}) - \frac{6}{ \pi}\ln(2) \ln(\sqrt{1+(\sqrt{3})^2}) + (\frac{3}{ \pi}\ln(2))^2arctg( \sqrt{3})) =$$$$ = \frac{3}{\pi}( \sqrt{3} - \frac{ \pi}{3} - \frac{6}{ \pi}\ln^2(2) + (\frac{3}{ \pi}\ln(2))^2\frac{ \pi}{3}) \approx 0,216 $$
–Ю—В–≤–µ—В: –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ–ґ–Є–і–∞–љ–Є–µ —А–∞–≤–љ–Њ \(D(x) = 0,216\)
–і) –Э–∞–є–і–µ–Љ —Б—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ \( \sigma_x\)
–°—А–µ–і–љ–µ–Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ –±—Г–і–µ–Љ –Є—Б–Ї–∞—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ \( \sigma_x = \sqrt{D(x)}\) $$\sigma_x = \sqrt{0,216} = 0.465 $$
–µ) –Э–∞–є–і–µ–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М \(P(x > M(x))\)
–Т–µ—А–Њ—П—В–љ–Њ—Б—В—М –њ–Њ–њ–∞–і–∞–љ–Є—П –Ј–љ–∞—З–µ–љ–Є–є —Б–ї—Г—З–∞–є–љ–Њ–є –≤–µ–ї–Є—З–Є–љ—Л \(X\) –≤ –Є–љ—В–µ—А–≤–∞–ї \(( \alpha; \beta)\) —А–∞–≤–љ–∞ \(P( \alpha < x < \beta) = \int_{ \alpha}^{ \beta}f(x)dx \). –Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –Є—Б—Е–Њ–і–љ—Л–µ –і–∞–љ–љ—Л–µ –≤ —Д–Њ—А–Љ—Г–ї—Г –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є $$ P( 0,662 < x < \sqrt{3}) = \int_{ 0,662}^{ \sqrt{3}}\frac{3}{\pi(1+x^2)}dx = \frac{3}{ \pi} arctg(x)|_{ 0,662}^{ \sqrt{3}} = \frac{3}{ \pi} ( arctg(\sqrt{3}) - arctg(0,662)) = \frac{1}{2} $$
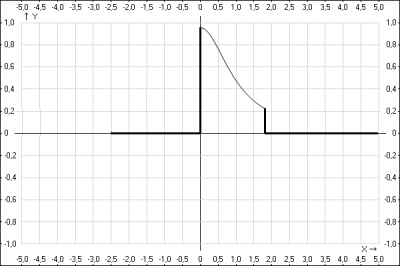
–У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –њ–ї–Њ—В–љ–Њ—Б—В–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П \(f(x)\)
–У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П \(F(x)\)