Задание: Около правильного треугольника описана окружность и в него вписана окружность. Сторона треугольника равна 4.
Вопрос: Найдите площадь кольца и длину меньшей окружности.
Решение:
1. Найдем площадь кольца.
Площадь кольца \( S_{к}\) равна разности площадей описанного \( S_{оп}\) круга и вписанного круга \( S_{вп}\) $$S_k = S_{оп} - S_{вп} \quad (1)$$Получили план решения задачи - находим площади вписанного круга и описанного около правильного треугольника круга. Для решения нарисуем рисунок
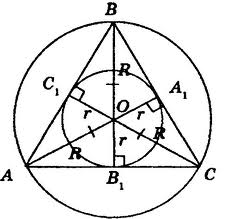
Найдем радиус вписанной окружности \(r = OB_1\) и радиус описанной окружности \(R = BO\). Воспользуемся свойством высот, медиан, биссектрис правильного треугольника - они совпадают и центр вписанной и описанной окружности лежит в точке пересечения высот, медиан и биссектрис правильного треугольника, т.е. \(BB_1\) - высота, медиана, биссектриса.
\( BB_1\) - высота, тогда треугольник \( ΔBB_1C\) - прямоугольный треугольник у которого известна сторона \(BC=4\),
\(BB_1\) - медиана, тогда она в т. \(B_1\) делит сторону \(AC\) на две равные части \(B_1C = \frac{1}{2}AC = \frac{1}{2}BC = 2\) .
По теореме Пифагора находим \(BB_1\), получаем $$BB_1 = \sqrt{BC^2 - B_1C^2} = \sqrt{16 - 4} = 2\sqrt{3}$$
\(BB_1\) - медиана, согласно свойств медиан: в точке пересечения медианы делятся в отношении \(2:1\), получаем, что $$r = OB_1 = \frac{1}{3}BB_1 = \frac{1}{3}2\sqrt{3} = \frac{2}{ \sqrt{3}}$$ тогда радиус описанной окружности равен $$R = BO = \frac{2}{3}BB_1 = \frac{2}{3}2\sqrt{3} = \frac{4}{ \sqrt{3}}$$Подставляем полученные радиусы в формулу площади круга \( S_{круга} = \pi r^2\), получаем $$S_{вп} = \pi r^2 = \pi (\frac{2}{ \sqrt{3}})^2 = \frac{4}{3} \pi$$$$S_{оп} = \pi R^2 = \pi (\frac{4}{ \sqrt{3}})^2 = \frac{16}{3} \pi$$Находим площадь кольца по формуле (1)$$ S_k = S_{оп} - S_{вп} = \frac{16}{3} \pi - \frac{4}{3} \pi =>$$$$ S_k = 4 \pi$$
Ответ: площадь кольца равна \(S_k = 4 \pi \)
Найдем длину меньшей окружности: радиус меньшей окружности уже нашли \(r = OB_1 = \frac{2}{ \sqrt{3}}\). Длинна окружности находится по формуле \(l_{окр} = 2\pi r\). Подставляем в формулу значение радиуса $$l_{окр} = 2\pi \frac{2}{ \sqrt{3}} = \frac{4}{ \sqrt{3}} \pi$$
Ответ: длина меньшей окружности равна \( l_{окр} = \frac{4}{ \sqrt{3}} \pi \)



