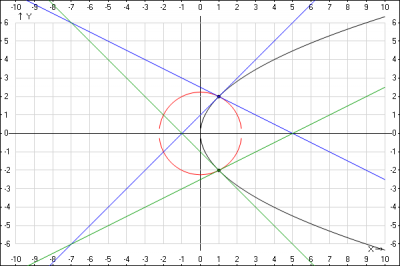
Для того, чтобы ответить на вопрос: "под каким углом пересекаются кривые",
найдем
1. координаты точек пересечения.
2. уравнения касательных к кривым в точках пересечения
3. угол между касательными
Решение:
1. найдем координаты точек пересечения, для этого решим систему уравнений $$ \begin{cases}x^2 + y ^2 = 5\\ y^2 =4x\end{cases} => \begin{cases}x^2 + 4x -5= 0\\ y^2 =4x\end{cases} => \begin{cases} x_1 = -5, x_2 =1\\ y^2 =4x\end{cases} => $$ Рассмотрим ОДЗ кривой \(y^2 = 4x\), т.к. \(y^2 > 0 \), то \(x > 0 \), т.е. корень \(x_1 = -5\) не подходит из -за ОДЗ кривой \(y^2 = 4x\), получаем $$\begin{cases} x =1\\ y_1 = -2; \quad y_2 = 2 \end{cases} => $$
получили две точки пересечения с координатами (1;-2) и (1;2).
2. найдем уравнения касательных в точках пересечения. Уравнение касательной \(y = f(x_0) + f'(x_0)(x-x_0)\).
Для уравнений касательных найдем производную функций по переменной \(x\)
\((x^2 + y ^2 - 5)' = 0 => 2x+2yy' =0 => y' = -\frac{x}{y}\) - производная уравнения окружности
\((y ^2 - 4x)' = 0 => 2yy' =4 => y' = \frac{2}{y}\) - производная параболы
Запишем уравнения касательных для точек пересечения
\((1;2)\) - касательная к параболе в точке\( y = 2 + \frac{2}{2}(x-1) => y = 1+x\) => \(k_2 = 1\)
\((1;2)\) - касательная к окружности в точке \( y = 2 -\frac{1}{2}(x-1) => y = \frac{5}{2} - \frac{1}{2}x\) => \(k_1 = -\frac{1}{2}\)
\((1;-2)\) - касательная к параболе в точке\( y = -2 + \frac{2}{-2}(x-1) => y = -1-x\) => \(k_2 = -1\)
\((1;-2)\) - касательная к окружности в точке \( y = -2 -\frac{1}{-2}(x-1) => y = -\frac{5}{2} + \frac{1}{2}x\) => \(k_1 = \frac{1}{2}\)
3. Угол между касательными находится по формуле \( tg(x) = \frac{k_2-k_1}{1+k_2*k_1}\)
для точки \((1;2)\) - \( tg(x) = |\frac{1+\frac{1}{2}}{1-1*\frac{1}{2}}| = 3 => x \approx 77^0 \)
для точки \((1;-2)\) - \( tg(x) = |\frac{-1-\frac{1}{2}}{1-1*\frac{1}{2}}| = 3 => x \approx 77^0 \)
Ответ: угол пересечения \( x \approx 77^0 \)
4. Графики кривых и касательных