
0 Голосов

|
 |
| Posted Февраль 13, 2013 by Вячеслав Моргун |
|
|
Проведем исследование функции \(y=3x^5-5x^3\). Общую схему исследования функции можно посмотреть в википедии и блоге "Порядок исследования функции и построения ее графика"
- Найдем область определения функции.
Областью определения функции \(f(x\)) называют множество всех значений x , для которых функция \(f(x)\) имеет смысл. В нашем примере степенная функция, областью определения является вся числовая ось.
Изучить симметрию графика, выяснить, является ли функция: четной, нечетной или ни той ни другой. \(f(-x)=3(-x)^5-5(-x)^3=-(3x^5-5x^3)=-f(x)\) - вывод функция нечетная, т.е. она симметрична относительно начала координат (0;0).
- Находим характерные точки графика.
- Точки пересечения с осью \(x\). Это точки при, которых \(y=0\).$$3x^5-5x^3=0 =>x^3(3x^2-5)=0 =>\begin{cases} x^3 = 0\\ 3x^2-5=0 \end{cases}=> \begin{cases} x = 0\\ x = \pm \sqrt{\frac{5}{3}} \end{cases}$$
- Точки пересечения с осью \(y\). Это точки при, которых \(x=0\).$$f(0)=3x^5-5x^3=3*0+5*0=0$$
- Найдем стационарные точки (или критические точки) - точки, в которых все частные производные обращаются в нуль.
Найдем производную от функции и приравняем ее к 0.$$(3x^5-5x^3)'=15x^4-15x^2=0 =>x^4-x^2=0 =>x^2(x^2-1)=0 \begin{cases} x^2 = 0\\ x^2-1=0 \end{cases}=>\begin{cases} x = 0\\ x=\pm 1 \end{cases}$$
Определим, являются эти точки экстремумами (максимума, минимума) или точками перегиба. Достаточным условием существования экстремумов (максимум, минимум) является изменение знака первой производной при переходе через точку экстремума.
Точка максимума знак меняется с "+" на "-" (функция монотонно возрастает до точки экстремума, а после нее монотонно убывает).
Точка минимума знак меняется с"-" на "+" (функция монотонно убывает до точки экстремума, а после нее монотонно возрастает).
Таким образом необходимо в окрестности стационарной точки в соответствующем интервале взять две точки (справа и слева от стационарной точки), подставить в производную и определить ее знак.
Рассмотрим полученные нами точки
- \(x=-1\) - точка слева \(f(-2)'=15x^4-15x^2=15*16-15*4 >0\), справа \(f(-\frac{1}{2})'=15x^4-15x^2=15*\frac{1}{16}-15*\frac{1}{4}\) - вывод это точка максимума.
- \(x=0\) - точка слева \(f(-\frac{1}{2})'=15x^4-15x^2=15*\frac{1}{16}-15*\frac{1}{4} < 0\), справа \(f(\frac{1}{2})'=15x^4-15x^2=15*\frac{1}{16}-15*\frac{1}{4} < 0\)- вывод это точка перегиба.
- \(x=1\) - точка слева \(f(\frac{1}{2})'=15x^4-15x^2=15*\frac{1}{16}-15*\frac{1}{4} < 0\), справа \(f(2)'=15x^4-15x^2=15*16-15*4 > 0\)- вывод это точка максимума.
- Исследуем функцию на монотонность
Достаточным условием возрастания (убывания ) функции является \(f`(x_0)>0\) или \(f`(x_0)\). Известно, что экстремумы - точки изменения монотонности. в п.4 было найдено 2 экстремума, значит у функции 3 интервала монотонности, рассмотрим их
- \((-\infty; -1)\) - функция монотонно возрастает (проверено в п. 4.1).
- \( (-1;1) \) - функция монотонно убывает (проверено в п. 4.2).
- \( (1 ;\infty) \) - функция монотонно возрастает (проверено в п. 4.3).
- Исследуем поведение функции при \(x \to +\infty\), \(x \to -\infty\). Т.к. функция определена на всей числовой оси, то асимптот у нее нет.
- \(x \to -\infty\) - \(\lim_{x \to -\infty}y=\lim_{x \to -\infty}(3x^5-5x^3)=-\infty\) - ось направлена вниз
- \(x \to +\infty\) -\(\lim_{x \to +\infty}y=\lim_{x \to +\infty}(3x^5-5x^3)=+\infty\) - ось направлена вверх
- Построение графика функции.
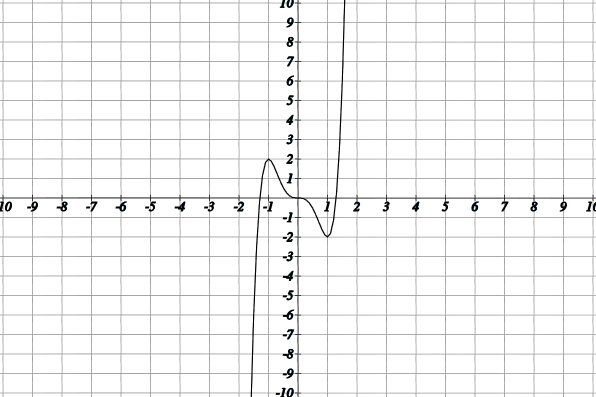
|
|



