Ищем наименьшее и наибольшее значения функции \( y= \ln(x^2-2x+4)\) на отрезке \([-1; \frac{3}{2}]\).
Наибольшим, наименьшим значением функции на отрезке могут быть точки минимума, максимума или значения функции на концах отрезка.
Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:
1. Находим стационарные точки:
Для нахождения стационарных точек найдем первую производную и приравняем ее у нулю $$y' = (\ln(x^2-2x+4))' =\frac{2x-2}{x^2-2x+4} = 2\frac{x-1}{x^2-2x+4}$$ приравняем производную к нулю $$ 2\frac{x-1}{x^2-2x+4} = 0 => x= 1$$
2 Выбираем из полученных стационарных точек те, которые принадлежат заданному отрезку.
В заданный отрезок попадает только точка \( x=1\) . Получили точку вероятного экстремума (минимума, максимума).
3. Находим значения функции в выбранной стационарной точке (см п.2).
Найдем значение функции в этой точке $$f(1)= \ln(1^2-2*1+4) = \ln(3) \approx 1.1$$
4. Находим значения функции на концах заданного отрезка:
$$f(-1)= \ln((-1)^2-2(-1)+4) = \ln(7) \approx 1.95$$
$$f( \frac{3}{2})= \ln(\frac{3}{2}^2-2\frac{3}{2}+4) = \ln(\frac{13}{4}) \approx 1.18$$
5. Из полученных значений функции (п.3 и п.4) выбираем наибольшее и наименьшее значения.
Сравниваем результаты, полученные в п.3 и п.4
Наибольшее значение функции на отрезке - значение функции в левой границе отрезка \(f(-1) = \ln(7) \approx 1.95\)
Наименьшее значение функции на отрезке - значение функции в стационарной точке \(f(1)= \ln(3) \approx 1.1\), которая оказалась точкой минимума, проверяем это, определяем знак первой производной слева и справа от стационарной точки.
\(f'(0) = 2\frac{0-1}{0^2-2*0+4} < 0 \),
\(f'(1.1) = 2\frac{1.1-1}{1.1^2-2*1.1+4} > 0 \),
получили, что производная изменила знак с \( - \quad 0 \quad + \), т.е. это действительно точка минимума.
Т.о. в данном типе задач необязательно выяснять, является ли стационарная точка точкой экстремума, достаточно найти значение функции в этой точке и сравнить со значениями функции на концах отрезка.
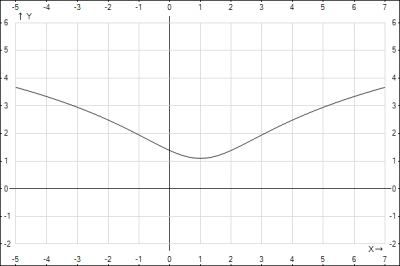
Проверяем полученный результат, строим график функции: