Решение: найдем максимальное значение функции x(t), т.е. экстремум функции на интервале \(t > 0 => \quad t \in (0;+\infty)\)
Схема исследования функции на максимум (экстремум).
1. Находим интервалы монотонности.
Найдем критические (стационарные) точки, для этого найдем первую производную и приравняем ее к нулю $$x'(t) = (-2(e^{-3t} - e^{-t}))'= -2(-3e^{-3t} + e^{-t}) = 2e^{-3t}(3 - e^{2t})$$ приравняем к 0 $$ 2e^{-3t}(3 - e^{2t}) = 0 => 3 - e^{2t} = 0 => $$$$ e^{2t} = 3 => 2t = \ln(3) => t = \frac{\ln(3)}{2} $$ функция имеет одну критическую (стационарную) точку на рассматриваемом интервале $$t = \frac{\ln(3)}{2}$$
2. Находим интервалы монотонности.
Функция имеет одну критическую точку, она делит рассматриваемый интервал на два интервала монотонности.
интервал \((0; \frac{\ln(3)}{2})\) найдем значение первой производной в любой точке интервала \(f(0.5) = 2e^{-3t}(3 - e^{2t}) > 0\), на этом интервале функция возрастает.
интервал \(( \frac{\ln(3)}{2}); +\infty)\) найдем значение первой производной в любой точке интервала \(f(1) = 2e^{-3t}(3 - e^{2t}) < 0\), на этом интервале функция убывает.
3. Экстремумы функции.
Достаточным условием существования экстремума является изменение знака производной при переходе через критическую точку.
для \(x = \frac{\ln(3)}{2} \): \(\quad + \quad 0 \quad -\), т.е. функция имеет точку максимума с координатами \(( \frac{\ln(3)}{2}; \frac{4}{3\sqrt{3}})\)
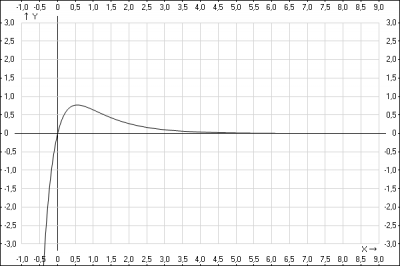
Ответ: максимальное значение \(x_{max}(t) = \frac{4}{3\sqrt{3}} \approx 0.77\) в момент времени \(t = \frac{\ln(3)}{2} \approx 0.55\)
График функции