Рассмотрим число $$ \log_{1.7}(0.5(1- \log_73))$$Это логарифм с основанием 1.7 > 1, т.е. это возрастающая функция см. рисунок.
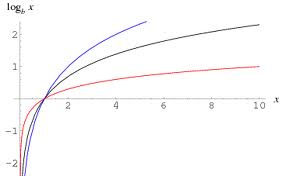
Из рисунка видно, что при x > 1 график функции логарифма находится выше оси Ox, т.е. число положительное, а при x < 1 график функции лежит ниже оси Ox, т.е. число отрицательное.
Т.о. чтобы определить знак числа, нужно аргумент сравнить с единицей. Предположим, что $$0.5(1- \log_73) < 1 => 1- \log_73 < 2 =>$$$$ - \log_73 < 1 => \log_73 > -1 =>$$$$ \log_73 > -\log_77 => 3 > \frac{1}{7}$$Получили истинное неравенство, т.е. \( 0.5(1- \log_73) < 1\), а это означает (см. рисунок), что число \( \log_{1.7}(0.5(1- \log_73)) < 0 \) отрицательное.



