1) длину стороны АБ.
Длину стороны АБ будем искать по формуле расстояния между точками $$d = \sqrt{ (x_2-x_1)^2 + (y_2-y_1)^2}$$ Подставляем координаты точек А(-3;-2), Б(1;6), получаем $$AB = \sqrt{ (1+3)^2 + (6+2)^2} = \sqrt{80} =4 \sqrt{5} \approx 8,84$$
2) уравнение прямой АБ.
Уравнения прямой будем искать как уравнение прямой, проходящей через две заданные точки $$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек А(-3;-2), Б(1;6) и получаем уравнение прямой $$ \frac{x+3}{1+3} = \frac{y+2}{6+2} => y = 2x +4$$
3) уравнение прямой АД.
Для уравнения прямой АД есть только координаты точки А(-3,-2), в то же время известно, что на этой прямой лежит основание трапеции, которое параллельно второму основание БС, а для этого основания известны две точки. Отсюда следует план нахождения уравнения прямой АД:
а) находим уравнение прямой БС как уравнение прямой, проходящей через две точки Б(1,6), С(9,2) $$\frac{x-1}{9-1} = \frac{y-6}{2-6} => y = -\frac{1}{2}x + \frac{13}{2}$$
б) прямые \(АД||БС\). Воспользуемся свойством угловых коэффициентов параллельных прямых - их угловые коэффициенты равны \(k_1=k_2\), т.е. $$k_{БС} = k_{АД} = -\frac{1}{2}$$
в) воспользуемся формулой уравнения прямой, проходящей через заданную точку в заданном направлении \( y - y_0 = k(x - x_0)\), подставляем координаты точки А(-3,-2) и угловой коэффициент $$ k_{АД} = -\frac{1}{2}$$ и получаем $$y +2 = -\frac{1}{2}(x + 3) => y = -\frac{1}{2}x -\frac{7}{2} $$
4) координаты точки Д, если ее абсцисса равна абсциссе точки С
В п.3 было найдено уравнение прямой АД \( y = -\frac{1}{2}x -\frac{7}{2} \) через которую проходит эта прямая. Из условия известны координаты точки С(9,2) и то, что координата точки Д(9;y). Подставим координату точки в уравнение прямой и найдем неизвестную координату \( y = -\frac{1}{2}*9 -\frac{7}{2} = -8\).
Получили координаты точки Д(9;-8).
5) величину угла \(\widehat{БСД}\)
Известны уравнения прямых, образующих угол \( \widehat{БСД} \) - прямые БС и СД. Угол между прямыми ищется по формуле $$ tg \phi = | \frac{k_2-k_1}{1+k_2k_1}|$$ Угловой коэффициенты прямой равен \(k_{БС} = -\frac{1}{2}\), а угловой коэффициент \(k_{СД}\) получим следующим образом. Есть две точки, через которые проходит прямая С(9,2) Д(9;-8), по условию задачи абсцисса у них одинаковая, а это означает, что прямая перпендикулярна оси Ox и проходит через точку x=9, а это и будет уравнение прямой СД. \(x = 0\), а это означает, что \(k_{СД} = tg(90^0) = \infty\), т.е. формула нахождения угла, которую я указал раннее применять нельзя. Угол будем искать исходя их следующих соображений:
прямая СД параллельна оси Oy. Пусть \( \alpha\) - угол который образует прямая БС с осью Ox, т.е. \( tg( \alpha) = k_{БС} = - \frac{1}{2} => \alpha \approx -27^0\), тогда искомый угол \(\widehat{БСД} = 90 + |\alpha| = 117^0 \)
6) расстояние от начала координат до всех сторон трапеции
расстояние от начала координат до всех сторон трапеции будем икать как расстояние от точки до прямой по формуле $$d = |\frac{Ax_0+By_0+C}{ \sqrt{A^2+B^2}}|$$ где Ax+By+C = 0 - уравнение прямой в общем виде, а \(x_0;y_0\) - координаты точки, расстояние от которой до прямой нужно найти, в данном случае координаты равны (0;0)
Приведем уравнение прямых сторон трапеции к общему виду и найдем расстояние
АБ: \( y = 2x +4 => y - 2x -4 = 0\), подставляем в формулу расстояния от точки до прямой $$d_{АБ} = |\frac{ 1*0 - 2*0 -4 }{ \sqrt{1^2+2^2}}| = \frac{4}{ \sqrt{5}} \approx 1,8$$
БС: \( y = -\frac{1}{2}x + \frac{13}{2} => 2y + x - 13 = 0\), подставляем в формулу расстояния от точки до прямой $$d_{БС} = |\frac{ 2*0 + 1*0 - 13 }{ \sqrt{1^2+2^2}}| = \frac{13}{ \sqrt{5}} \approx 5,8$$
СД: уравнение прямой СД x = 9, т.е. расстояние до прямой равно \(d_{СД} = 9 \)
АД: \( y = -\frac{1}{2}x -\frac{7}{2} => 2y + x + 7 = 0\), подставляем в формулу расстояния от точки до прямой $$d_{БС} = |\frac{ 2*0 + 1*0 + 7 }{ \sqrt{1^2+2^2}}| = \frac{7}{ \sqrt{5}}$$
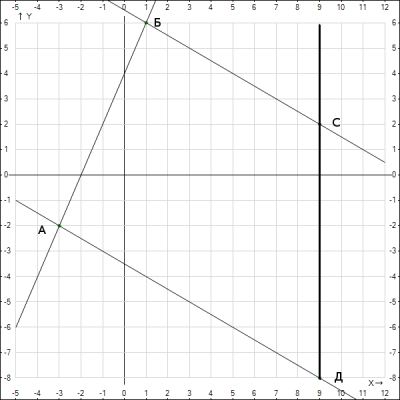
7) Нанесем координаты точек и прямых на декартовую систему координат.