1) уравнение медианы, высоты, проведенной из вершины \(A_0\).
Уравнение медианы. Будем искать по формуле уравнения прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} \quad (1)$$ Одна точка \(A_0(2;5)\), вторая точка M - середина между точками \(A_1(3;3)\) и \(A_2(-1;4)\), координаты которой находятся по формуле \(M(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2})\) подставляем координаты и получаем \(M(\frac{3-1}{2};\frac{3+4}{2}) =>\) координаты искомой точки \(M(1;3,5)\) подставляем координаты точек A и M в уравнение (1) и получаем уравнение медианы $$\frac{x-2}{1-2}=\frac{y-5}{3,5-5} => y = \frac{3}{2}x + 2$$
Уравнение высоты. Уравнение высоты будем искать по формуле уравнения прямой, проходящей через заданную точку в заданном направлении $$y - y_0 = k(x - x_0) \quad (2)$$ где заданная точка - точка \(A_0\), а заданное направление - угловой коэффициент прямой, который будем искать воспользовавшись свойством угловых коэффициентов двух перпендикулярных прямых $$k_1 = -\frac{1}{k_2} \quad (3)$$ Высота, опущенная из вершины \(A_0\) - будет перпендикулярна прямой \(A_1A_2\), а уравнение этой прямой и соответственно ее угловой коэффициент легко получить, применив формулу уравнения прямой проходящей через две заданные точки. Найдем уравнение прямой \(A_1A_2\), подставим координаты \(А_1(3,3), А_2(-1,4)\) в уравнение прямой (1) $$\frac{x-3}{-1-3}=\frac{y-3}{4-3} => y = -\frac{1}{4}x +\frac{15}{4}$$ Теперь применим свойство угловых коэффициентов перпендикулярных прямых (3) и получим угловой коэффициент высоты \(k_h = -\frac{1}{k_{A_1A_2}} = -\frac{1}{-\frac{1}{4}} = 4\). Координаты точки \(A_0(2;5)\) и угловой коэффициент подставим в уравнение прямой, проходящей через заданную точку в заданном направлении (2) и получим уравнение высоты $$y - 5 = 4(x - 2) => y = 4x - 3$$
2) уравнение средней линии EF, параллельной основанию \(A_1A_2\).
Средняя линия делит стороны треугольника пополам, т.е. уравнение средней линии можно найти как уравнение прямой, проходящей через две заданные точки, а координаты этих точек находятся также как координаты точки M (см. п.1). Т.к. уравнение прямой \(A_1A_2\) было найдено в п.2, а средняя линия параллельна этой прямой то их угловые коэффициенты равны \(k_1=k_2 = -\frac{1}{4}\), если мы найдем координаты одной точки, то воспользовавшись уравнением (2) - уравнением прямой, проходящей через заданную точку в заданном направлении, получим искомое уравнение средней линии. Найдем одну из точек средней линии E - середину стороны \(A_0A_1\). \(E(\frac{x_1+x_0}{2};\frac{y_1+y_0}{2}) => E(\frac{3+2}{2};\frac{3+5}{2}) => E(2,5; 4) \). Подставляем в уравнение (2) и находим уравнение средней линии EF$$y - 4 = -\frac{1}{4}(x-2,5) => y = -\frac{1}{4}x + \frac{37}{8}$$
3) угол между медианой и основанием и стороной \(A_1A_2\).
Уравнение медианы: \(y = \frac{3}{2}x + 2\), где \(k_1 = \frac{3}{2}\)
Уравнение основания \(A_1A_2\): \(y = -\frac{1}{4}x +\frac{15}{4}\), где \(k_2 = -\frac{1}{4}\)
Угол между прямыми рассчитывается по формуле $$tg\phi = \frac{k_2-k_1}{1+k_2*k_1}$$ подставляем угловые коэффициенты $$tg\phi = |\frac{-\frac{1}{4}-\frac{3}{2}}{1-\frac{1}{4}\frac{3}{2}}| = \frac{14}{5} = 2,8 => \phi = arctg(2,8) \approx 70^0$$
4) вычислить длину найденной высоты.
Длина высоты - расстояние от точки до прямой, т.е. от точки \(A_0(2;5)\) до стороны \(A_1A_2\), уравнение которой \(y = -\frac{1}{4}x +\frac{15}{4} => 4y + x -15 =0\). Расстояние от точки до прямой рассчитывается по формуле $$d= \frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}$$ где \(x_0;y_0\) - координаты точки \(A_0(2;5)\), а \(Ax+By+C\) - уравнение прямой \(A_1A_2\). Подставляем данные и получаем $$d= \frac{4*5 + 2 -15}{\sqrt{4^2+1^2}} = \frac{7}{\sqrt{17}} \approx 1.7$$Длина высоты равна \(d = 2\frac{1}{3}\)
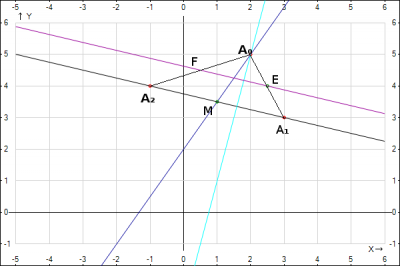
5) Решение проверить графически.
Наносим все точки и прямые на декартовую систему координат