Рассмотрим два случая:
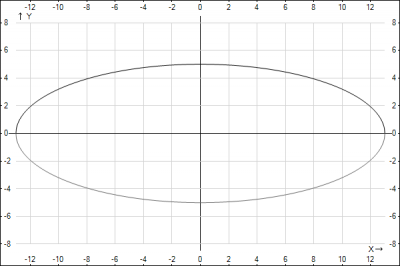
1. Пусть большая ось совпадаем с осью Ox, Тогда малая полуось равна \(b = \frac{10}{2}=5\), а эксцентриситет рассчитывается по формуле $$\epsilon=\frac{c}{a} = \sqrt{1-(\frac{b}{a})^2} => \epsilon^2 = 1-(\frac{b}{a})^2 =>$$$$ a = \frac{b}{\sqrt{1- \epsilon^2 }}$$ Подставляем данные задачи $$a = \frac{5}{\sqrt{1- (\frac{12}{13})^2 }} = \frac{5*13}{\sqrt{169-144}} = \frac{5*13}{\sqrt{25}}=13$$
Подставляем значение полуосей в каноническое уравнение эллипса $$\frac{x^6}{13^2}+\frac{y^2}{5^2}=1$$
Строим эллипс
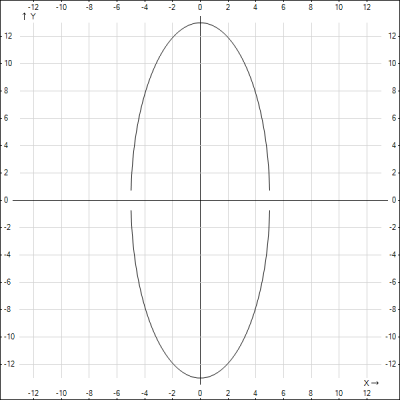
2. Пусть большая ось совпадаем с осью Oy, Тогда малая полуось равна \(a = \frac{10}{2}=5\), а большая полуось тогда будет равна \(b = 13\), т.е поменяли их местами.
Можно провести расчеты аналогично п. 1 и убедиться в правильности результата. Эксцентриситет рассчитывается по формуле $$\epsilon=\frac{c}{b} = \sqrt{1-(\frac{a}{b})^2} => \epsilon^2 = 1-(\frac{b}{a})^2 =>$$$$ b = \frac{a}{\sqrt{1- \epsilon^2}}$$ Подставляем данные задачи $$b = \frac{5}{\sqrt{1- (\frac{12}{13})^2 }} = \frac{5*13}{\sqrt{169-144}} = \frac{5*13}{\sqrt{25}}=13$$
Подставляем значение полуосей в каноническое уравнение эллипса $$\frac{x^6}{5^2}+\frac{y^2}{13^2}=1$$
Строим эллипс