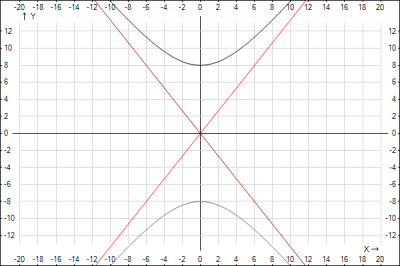
Каноническое уравнение гиперболы \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\). Для построения гиперболы необходимо найти полуоси, для этого у нас есть уравнение асимптот $$y = \pm \frac{4}{3}x = \pm \frac{b}{a}x => \frac{b}{a} = \frac{4}{3}$$ и расстояние между фокусами \(2с = 20 => c=10\), которое связано с полуосями формулой $$c^2=a^2+b^2 => a^2+b^2 = 100$$ Получили два уравнения, которые объединим в систему уравнений и решим ее $$\begin{cases}a^2+b^2 = 100\\ \frac{b}{a} = \frac{4}{3}\end{cases} => \begin{cases}a^2+(\frac{4}{3}a)^2 = 100\\ b = \frac{4}{3}a\end{cases} => $$$$ \begin{cases}a^2+\frac{16}{9}a^2 = 100\\ b = \frac{4}{3}a\end{cases} => \begin{cases}\frac{25}{9}a^2 = 100\\ b = \frac{4}{3}a\end{cases} => $$$$ \begin{cases} a =6\\ b =8\end{cases}$$ Получили полуоси \(a = 6\), \(b=8\). Подставляем значения полуосей в каноническое уравнение гиперболы $$\frac{x^2}{36}-\frac{y^2}{64}=1$$
Строим гиперболу
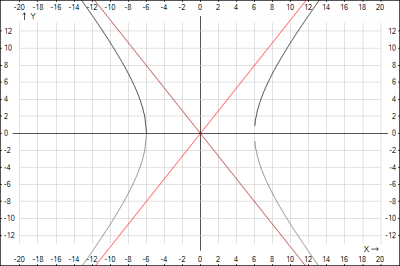
В задании ничего не говорится о сопряженной гиперболе, поэтому построим и ее. Сопряженная гипербола - гипербола у которой ось Oy - действительная ось, а ось Ox - мнимая, а каноническое уравнение имеет вид $$\frac{x^2}{36}-\frac{y^2}{64}=-1$$
Строим сопряженную гиперболу