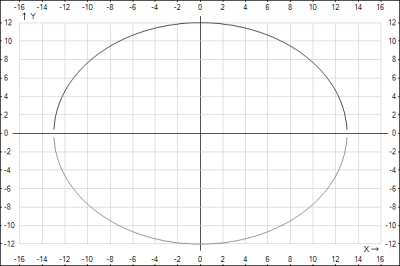
Каноническое уравнение эллипса имеет вид $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$ В задаче дана малая ось 2b=24 => b=12, а расстояние между фокусами 2c=10 => c=5. Нужно найти большую полуось a. Найдем ее из формулы, связывающей полуоси $$a^2=b^2+c^2 => a^2 = 12^2+5^2 => a^2= 169 => a=13$$ Подставляем полуоси в каноническое уравнение эллипса $$\frac{x^2}{13^2}+\frac{y^2}{12^2}=1$$Строим эллипс.
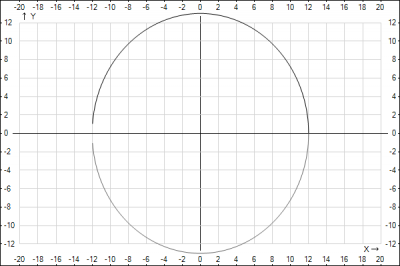
Также необходимо помнить о том, что большой полуосью может быть \(b\), а \(a\) - малой полуосью, тогда каноническое уравнение эллипса будет иметь вид $$\frac{x^2}{12^2}+\frac{y^2}{13^2}=1$$
Строим эллипс.