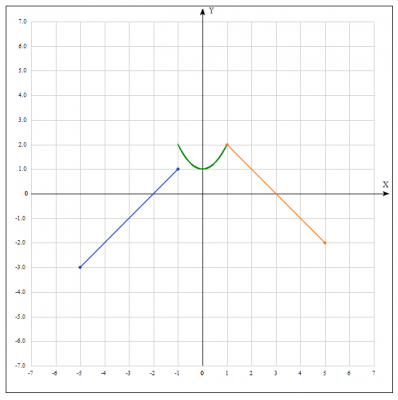
Решение: исследуем функцию \( y = \begin{cases} x+2 & x \leq -1\\ x^2+1 & -1 < x < 1 \\ -x+3 & x \geq 1 \end{cases}\) на непрерывность и построим ее график.
Функция состоит из элементарных функций, которые непрерывны на числовой оси, поэтому точками возможного разрыва могут быть только точки, в которых меняется аналитическое выражение функции, т.е. \(x = -1; x = 1\).
Проанализируем поведение функции в этих точках.
Точка \(x= -1\)
В окрестности точки \(x= -1\) функция определена двумя различными выражениями:
слева \(f(x) = x+2 \) и
справа \(f(x) = x^2+1 \)
Вычислим в этой точке:
1. левосторонний предел функции \(f(x) = x+2\): $$ \lim_{x \to -1-0}f(x) = \lim_{x \to -1-0}(x+2) = 1$$
2. правосторонний предел функции \(f(x) = x^2+1 \): $$\lim_{x \to -1+0}f(x) = \lim_{x \to -1+0}( x^2+1) = 2$$
3. значение функции в точке: $$f(-1) =(x+2)|_{x=-1} = 1$$
Таким образом получили, что односторонние пределы существуют, конечные, но не равны между собой, т.е. в точке \(x = -1\) функция имеет разрыв первого рода, скачек функции равен 1.
Точка \(x= 1\)
В окрестности точки \(x= 1\) функция определена двумя различными выражениями:
слева \(f(x) = x^2+1 \) и
справа \(f(x) = -x+3 \)
Вычислим в этой точке:
1. левосторонний предел функции \(f(x) = x^2+1\): $$ \lim_{x \to 1-0}f(x) = \lim_{x \to 1-0}(x^2+1) = 2$$
2. правосторонний предел функции \(f(x) = -x+3 \): $$\lim_{x \to 1+0}f(x) = \lim_{x \to 1+0}( -x+3) = 2$$
3. значение функции в точке: $$f(1) =(-x+3)|_{x=1} = 2$$
Таким образом получили, что односторонние пределы существуют, конечные и равны между собой и равны значению функции в этой точке, т.е. в точке \(x=1\) функция непрерывна.
Построим схематически график функции: