1. Вычислить длину медианы АМ.
Для нахождения длины медианы найдем координату точки M, зная координаты точки A найдем расстояние между этими точками, которое рассчитывается по формуле $$d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \quad (1)$$Найдем координаты точки M, которая находится по середине между точками B(1;-1) и C(3;5), координаты рассчитываются по формуле $$M(\frac{x_B+x_C}{2};\frac{y_B+y_C}{2})$$ подставляем значения координат и получаем $$M(\frac{1+3}{2};\frac{-1+5}{2}) => M(2;2)$$ Найдем длину медианы, подставим координаты точек в формулу (1) $$d_{AM} = \sqrt{(8-2)^2+(0-2)^2} = 2\sqrt{10}$$
2. Уравнение медианы AM.
Известны две точки A и M через которые проходит медиана. Для составления уравнения медианы, воспользуемся формула уравнения прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$ Подставляем координаты точек и получаем уравнение медианы$$\frac{x-8}{2-8}=\frac{y-0}{2-0} => y = -\frac{1}{3}x+\frac{8}{3}$$
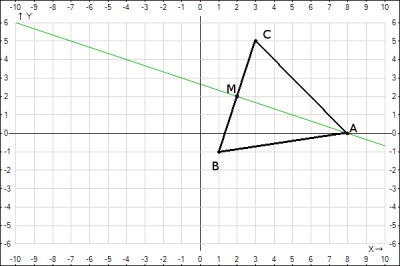
3. Наносим полученные точки и уравнение прямой на декартовую систему координат.