Запишем формулу канонического уравнения эллипса $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$ Нам необходимо найти полуоси эллипса, чтобы получить искомое уравнение.
Рассмотрим два случая:
1. Фокальная ось совпадает с осью Ox, т.е. большая полуось - a .
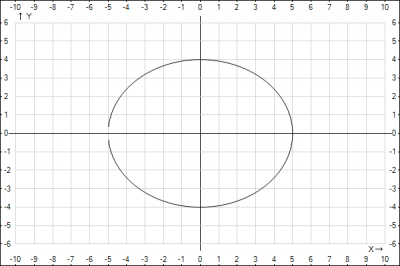
В условии задачи дан эксцентриситет, т.к. большая полуось - a, то эксцентриситет рассчитывается по формуле $$\epsilon =\frac{c}{a} = \frac{3}{5} => a = \frac{5}{3}*\frac{6}{2} => a = 5$$Осталось найти вторую полуось b, для этого воспользуемся формулой, связывающей фокальное расстояние и полуоси $$a^2-c^2=b^2$$подставляем и получаем длину полуоси b$$b=\sqrt{25-9}=4$$ Получили уравнение эллипса $$\frac{x^2}{25}+\frac{y^2}{16}=1$$
Строи эллипс
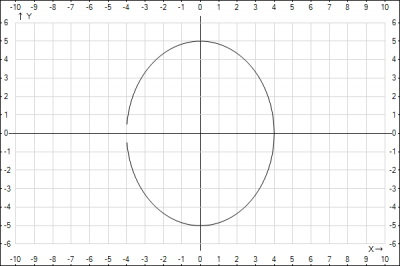
2. Фокальная ось совпадает с осью Oy, т.е. большая полуось - b .
В условии задачи дан эксцентриситет, т.к. большая полуось - b, то эксцентриситет рассчитывается по формуле $$\epsilon =\frac{c}{b} = \frac{3}{5} => b = \frac{5}{3}*\frac{6}{2} => b = 5$$Осталось найти вторую полуось a, для этого воспользуемся формулой, связывающей фокальное расстояние и полуоси $$b^2-c^2=a^2$$подставляем и получаем длину полуоси b$$b=\sqrt{25-9}=4$$ Получили уравнение эллипса $$\frac{x^2}{16}+\frac{y^2}{25}=1$$
Строи эллипс