Рішення: розглянемо умову задачі: уявна вісь гіперболи дорівнює 8, при цьому не вказано яка це вісь 2a = 8 або 2b = 8, тобто потрібно розглядати два випадки:
1. уявна вісь гіперболи - 2b
Розглянемо канонічне рівняння гіперболи, при якому 2b - уявна вісь $$ \frac{x ^ 2}{a ^ 2} - \frac{y ^ 2}{b ^ 2} = 1 \quad (1) $$ знак мінус стоїть перед змінною \(y \), це означає, що дійсна вісь - вісь \(2a \), яка лежить на осі симетрії Ox, уявна вісь - вісь \(2b \), яка лежить на осі симетрії Oy.
Згідно умови завдання, відстань між фокусами \(2c = 10 = > c = 5 \). Скористаємося співвідношенням між півосями \(a, b \) і фокальною відстанню \(2c \) гіперболи $$ c ^ 2 = a ^ 2 + b ^ 2 \quad (2) $$ підставляємо відомі значення: згідно умови завдання, фокальна відстань \(2c = 10 => c = 5 \), а уявна вісь дорівнює \(2b = 8 => b = 4 \). Знайдемо дійсну піввісь, підставляємо дані в (2) $$ 5 ^ 2 = a ^ 2 + 4 ^ 2 => a = \sqrt{25-16} => a = 3 $$ Рішення підставляємо в рівняння (1), отримуємо рівняння гіперболи $$ \frac{x ^ 2}{3 ^ 2} - \frac{y ^ 2}{4 ^ 2} = 1 = > \frac{x ^ 2}{9} - \frac{y ^ 2}{16} = 1 $$
Відповідь: рівняння гіперболи, у якої уявна піввісь - \(b \), дорівнює \( \frac{x ^ 2}{9} - \frac{y ^ 2}{16} = 1 \)
2. уявна вісь гіперболи - 2a
Розглянемо канонічне рівняння гіперболи, при якому 2a - уявна вісь $$ \frac{y ^ 2}{b ^ 2} - \frac{x ^ 2}{a ^ 2} = 1 \quad (3) $$ знак мінус стоїть перед змінною \(x \), це означає, що дійсна вісь - вісь \(2b \), яка лежить на осі симетрії Oy, уявна вісь - вісь \(2a \), яка лежить на осі симетрії Ox.
Згідно умови завдання, відстань між фокусами \(2c = 10 = > c = 5 \). Скористаємося співвідношенням між півосями \(a, b \) і фокальною відстанню \(2c \) гіперболи $$ c ^ 2 = a ^ 2 + b ^ 2 \quad (2) $$ підставляємо відомі значення: згідно умови завдання, фокальна відстань \(2c = 10 => c = 5 \), а уявна вісь дорівнює \(2a = 8 = > a = 4 \). Знайдемо дійсну піввісь, підставляємо данні в (2) $$ 5 ^ 2 = a ^ 2 + 4 ^ 2 => b = \sqrt{25-16} => b = 3 $$ Рішення підставляємо в рівняння (3), отримуємо рівняння гіперболи $$ \frac{y ^ 2}{3 ^ 2} - \frac{x ^ 2}{4 ^ 2} = 1 => \frac{y ^ 2}{9} - \frac{x ^ 2}{16} = 1 $$
Відповідь : рівняння гіперболи, у якої уявна піввісь - \(a \), дорівнює \( \frac {y ^ 2}{9} - \frac{x ^ 2}{16} = 1 \)
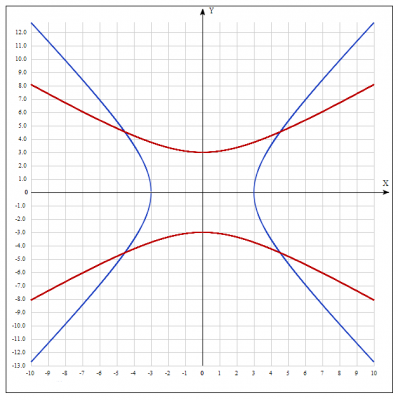
3. Будуємо гіперболу.