1. Написать уравнение касательной к кривой $$y=2x^3-3x^2+x-2$$ в точке x=1.
Уравнение касательной находится по формуле \(y = f(x_0)+f'(x_0)(x-x_0)\).
Найдем значение функции в этой точке \(f(1) = 2*1^3-3*1^2+1-2 = -2\).
Найдем первую производную функции $$f(x) = (2x^3-3x^2+x-2)' = 6x^2-6x+1$$ найдем значение производной в этой точке \(f'(1) = 6*1^2-6*1+1 = 1\)
Подставляем полученные данные в уравнение касательной $$y = -2 + x-1 => y = x-3$$ получили уравнение касательной к графику функции в заданной точке.
2. Написать уравнение нормали к кривой $$y=2x^3-3x^2+x-2$$ в точке x=1. В пункте 1 было найдено уравнение касательной, как известно нормаль к кривой в точке касания перпендикулярен касательной, т.е. их угловые коэффициенты связаны отношением \(k_1=-\frac{1}{k_2}\) найдем угловой коэффициент нормали $$k_n=-\frac{1}{k_k} = -\frac{1}{1}=-1$$ У нас есть точка с координатами (1;-2) - точка касания, через которую проходит нормаль и ее направление \(k_n=-1\), для написания уравнения нормали воспользуемся уравнением прямой, проходящей через заданную точку в заданном направлении $$y - y_0 = k(x-x_0)$$ подставляем данные и получаем $$y+2=-1*(x-1) => y = -x+1-2 => y = -x-1$$
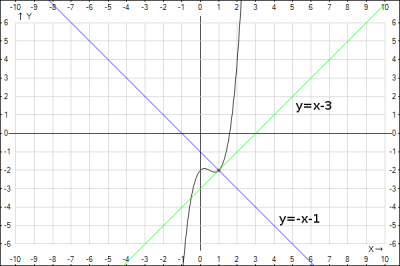
3. Построим график функции, касательную и нормаль для проверки правильности решения.