Записать уравнение кривой в каноническом виде. Найти координаты фокусов, вершин центра.

Дано уравнение кривой второго порядка \(25y^2-4x^2+24x+50y-86=0\)

1. Записать уравнение кривой в каноническом виде.
В данном уравнении есть только члены второй и первой степени (нет смешанного произведения), поэтому каноническое уравнение будем получать методом выделения полного квадрата.
$$25y^2-4x^2+24x+50y-86=0=> 25y^2+50y-4x^2+24x-86=0=>  $$$$ 25(y^2+2y)-4(x^2-6x)-86=0 => 25(y^2+2y+1-1)-4(x^2-2*3x+9-9)-86=0 => $$$$ 25(y+1)^2-25-4(x-3)^2+36-86=0 => 25(y+1)^2-4(x-3)^2 =75 $$осталось последнее действие - разделим обе части уравнения на 75 $$\frac{(y+1)^2}{3}-\frac{(x-3)^2}{\frac{75}{4}}=1$$Получили уравнение гиперболы, Каноническое уравнение гиперболы $$\frac{y^2}{b^2}-\frac{x^2}{a^2}=1$$Для того, чтобы привести к указанному виду введем новые координаты \(x'=x-3;y'=y+1\), подставляем и получаем каноническое уравнение в новой системе координат, которая смещена относительно первичной системы координат на по оси Ох вправо на  3 и по оси Оу на 1 вниз, получаем $$\frac{(y')^2}{3}-\frac{(x')^2}{\frac{75}{4}}=1$$При этом действительная ось лежит на оси Oy, действительная полуось равна\(b =\sqrt 3\) , а мнимая на оси Ox, мнимая полуось равна \(a = \frac{5}{2}\sqrt 3\).

2. Найти координаты фокусов, вершин, центр.
Рассмотрим полученное уравнение гиперболы. \(\frac{(y+1)^2}{3}-\frac{(x-3)^2}{\frac{75}{4}}=1\) .
Точка пересечения осей симметрии - центр гиперболы. Координаты центра \(O(3;-1)\)
Точки пересечения с осью, в данном случае с осью Oy - вершины гиперболы, т.е. при x=3 $$\frac{(y+1)^2}{3} = 1 => y = \pm \sqrt{3} -1$$, т.е. координаты вершины равны $$A_1(3;\sqrt{3} -1); A_2(3;-\sqrt{3} -1)$$Координаты фокусов гиперболы с центром в начале координат (x';y') равны \(F_1(0;c);F_2(0;-c)\), где фокусное расстояние находятся по формуле \(c^2=a^2+b^2\) подставляем значения полуосей и получаем $$c = \sqrt{3+\frac{75}{4}} = \sqrt{\frac{87}{4}}$$ т.к. по условию задачи центра смещен \(x'=x-3;y'=y+1\) => \(x=x'+3;y=y'-1\) координаты фокусов будут равны \(F_1(3;-c-1);F_2(3;c-1)\) ,  т.е. координаты фокусов в первичной системе координат равны \(F_1(3;\sqrt{\frac{87}{4}}-1);F_2(3;-\sqrt{\frac{87}{4}}-1)\)

3.Записать уравнение директрис и асимптот
Асимптоты. Уравнения асимптот равны \(y'= \pm \frac{b}{a}x\), с учетом сдвига системы координат \(y+1 = \pm \frac{\sqrt{3}}{\frac{5}{2}\sqrt{3}}(x-3) => y = \pm \frac{2}{5}(x-3) -1\) Получили два уравнения асимптоты $$y_1 = -\frac{2}{5}x +\frac{1}{5}$$ и $$y_2 = \frac{2}{5}x -\frac{11}{5}$$
Уравнение директрисы для системы координат \(x';y'\) находится по формуле \(y = \pm \frac{b}{\epsilon} = \pm \frac{b}{\frac{c}{b}} = \pm \frac{b^2}{c}\) С  учетом сдвига получаем $$y+1= \pm \frac{3}{\sqrt{\frac{87}{4}}} = \pm \frac{6}{\sqrt{87}} =>$$первое уравнение директрисы $$y_{d1} = \frac{6}{\sqrt{87}}-1 \approx -0.36$$второе уравнение директрисы $$y_{d2} = -\frac{6}{\sqrt{87}}-1 \approx -1.64$$

4. Построить рисунок:

Дано уравнение кривой второго порядка \(9x^2+4y^2+54x+24y+81=0\)

1. Записать уравнение кривой в каноническом виде.
В данном уравнении есть только члены второй и первой степени (нет смешанного произведения), поэтому каноническое уравнение будем получать методом выделения полного квадрата.
$$9x^2+4y^2+54x+24y+81=0 => 9x^2+54x+4y^2+24y+81=0 =>  $$$$ 9(x^2+6x)+4(y^2+6y)+81=0 => 9(x^2+2*3x+9-9)+4(y^2+2*3y+9-9)+81=0 => $$$$ 9(x+3)^2-81+4(y+3)^2-36+81=0 => 9(x+3)^2+4(y+3)^2=36$$осталось последнее действие - разделим обе части уравнения на 36 $$\frac{(x+3)^2}{4}+\frac{(y+3)^2}{9}=1$$Получили уравнение эллипса, Каноническое уравнение эллипса $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$Для того, чтобы привести к указанному виду введем новые координаты \(x'=x+3;y'=y+3\), подставляем и получаем каноническое уравнение в новой системе координат, которая смещена относительно базовой системы координат на по оси Ох на влево 3 и по оси Оу на 3 вниз, получаем $$\frac{(x')^2}{4}+\frac{(y')^2}{9}=1$$

2. Найти координаты фокусов, вершин центра.
Рассмотрим полученное уравнение эллипса. \(\frac{(x+3)^2}{4}+\frac{(y+3)^2}{9}=1\) из уравнения видно, что координата центра эллипса O(-3;-3)
Также из уравнения определим полуоси эллипса  \(a^2=4 => a=2\)  и \(b^2=9 => b=3\).
Найдем координаты фокусов. Определим, на какой оси лежит фокальная ось \(F_1F\). Т.к. b > a, то фокальная ось лежит на оси Oy, поэтому координаты фокусов будут следующими:  \(F_1(0;-с)\) и \(F_2(0;c)\), где \(c=\sqrt{b^2-a^2} => c=\sqrt{9-4}=\sqrt{5}\), т.е. координаты фокусов будут равны \(F_1(0;-\sqrt{5})\) и \(F_2(0;\sqrt{5})\)

\pm \frac{9}{\sqrt{5}}
Т.к. b > a , то уравнение директрисы имеет вид \(y \pm \frac{b^2}{c}\) , подставляем данные и получаем $$y = \pm \frac{9}{\sqrt{5}}$$ Это уравнение мы получили для канонического уравнения эллипса с центром в начале координат, а мы помним связь между базовой системой координат и новой системой координат \(x'=x+3;y'=y+3\). Т.е. уравнение для базовой системы координат примет вид $$y+3 = \pm \frac{9}{\sqrt{5}} => y = \pm \frac{9}{\sqrt{5}} - 3$$

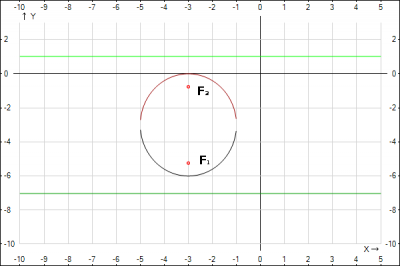
4. Построить рисунок: