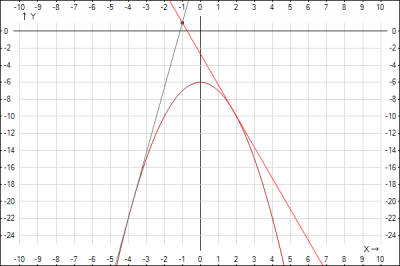
В данной задаче говорится о касательной как о прямой, проходящей через заданную точку. Запишем уравнение прямой, проходящей через заданную точку в заданном направлении $$y-y_0=k(x-x_0)$$По условию задачи, точка через которую проходит эта прямая (касательная) это точка с координатами M(-1;1), подставляем и получаем уравнение $$y-1=k(x+1) \quad (1)$$Т.о. чтобы закончить составление уравнения касательной необходимо найти угловой коэффициент \(k\). Вернемся к известному уравнению касательной $$y = f(x_0)+f'(x_0)(x-x_0)$$ Угловым коэффициентом касательной является производная функции в точке касания, т.е. \(k = f'(x_0)\). Т.е. нам нужно найти производную функции в точке касания, находим $$y'=(-x^2-6) = -2x => f'(x_0) = -2x_0$$Подставляем в уравнение касательной (1) и получаем $$y-1=-2x_0(x+1) => y=-2x_0(x+1)+1 \quad (2)$$ Теперь найдем точку касания. Точка касания - общая точка касательной и функции, поэтому для ее нахождения составим систему уравнения при этом мы учитываем, что в точке касания \(x=x_0\), получим $$\begin{cases} y=-x^2-6 \\y-1=-2x(x+1)\end{cases}=>\begin{cases} y=-x^2-6 \\ -x^2-6-1=-2x^2x-2x \end{cases}=> $$$$ \begin{cases} y=-x^2-6 \\ x^2+2x-7=0 \end{cases}=> \begin{cases} y=-x^2-6 \\ x_{1,2}=-1 \pm 2\sqrt{2} \end{cases}$$ Для решения задачи нас интересует только координата x. Мы получили две координаты т.е. будет две касательные. Подставляем в уравнение (2) и получаем первое уравнение прямой$$y = -2(-1+2\sqrt{2})(x+1) +1 $$ и второе уравнение прямой $$y = -2(-1- 2\sqrt{2})(x+1) +1$$Построим график функции и его две касательные, проходящие через заданную точку M(-1;1)