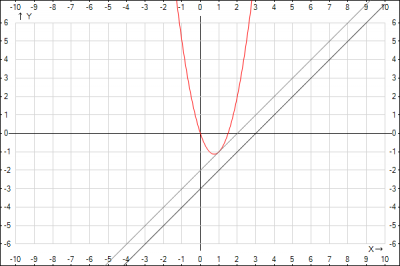
Запишем уравнение касательной $$y = f(x_0) + f'(x_0)(x-x_0)$$ в уравнении касательной \(x_0\) - координата точки касания. Она не известно, поэтому найдем ее. В условии сказано, что касательная параллельна прямой \(y = x-3\). Если две прямые параллельны, то их угловые коэффициенты равны, т.е. угловой коэффициент касательной \(f'(x_0)\) равен угловому коэффициенту прямой \(y = x-3\), который равен \(k = 1\), т.е. получаем \(f'(x_0) = 1\). Т.е. най необходимо найти производную функции и приравнять ее к одному и решить полученное уравнение $$f'(x_0) = (2x_0^2 –3x_0)'=1 => 4x_0-3=1 =>x_0 = 1$$ Получили координату точки касания. Теперь найдем значение функции в этой точке $$f(x_0) = f(1) = 2*1^2-3*1 = -1$$Подставляем полученный данные в уравнение касательной и получим $$y = f(x_0) + f'(x_0)(x-x_0) = -1 +1*(x-1) =>$$$$y = x -2$$Строим графики, проверяем правильность решения