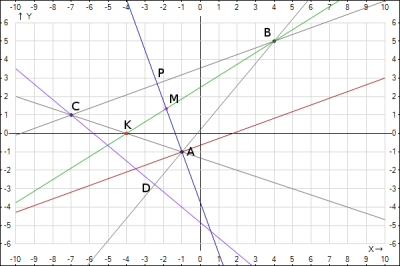
Найти:
1. Уравнения сторон треугольника AB, AC, BC
При известных двух вершинах уравнение сторон находится по формуле прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}$$ подставляем координаты точек и получаем
уравнение стороны AB: \(\frac{x+1}{4+1} = \frac{y+1}{5+1} => \frac{6x}{5}+\frac{6}{5}-1 = y => \)$$AB: \quad y= \frac{6}{5}x+\frac{1}{5}$$
уравнение стороны AC: \(\frac{x+1}{-7+1} = \frac{y+1}{1+1} => -\frac{x}{3}-\frac{1}{3}-1 = y => \)$$AC: \quad y= -\frac{1}{3}x-\frac{4}{3}$$
уравнение стороны BC: \(\frac{x-4}{-7-4} = \frac{y-5}{1-5} => \frac{4x}{11}-\frac{16}{11}+5 = y => \)$$BC: \quad y= \frac{4}{11}x+\frac{39}{11}$$
2. Уравнение медианы BK.
Для уравнения медианы одна точка известна B, а вторую найдем как середина между точками A и C. Координаты точки \(K(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2})\), подставляем координаты точек A и C и получаем \(K(\frac{-1-7}{2};\frac{-1+1}{2})\) => $$K(-4; 0)$$
Уравнение медианы получаем из формулы уравнения прямой, проходящей через две заданные точки BK: \(\frac{x+4}{4+4} = \frac{y+0}{5+0} => \frac{5x}{8}+\frac{5}{2} =y => \) $$BK: \quad y= \frac{5}{8}x+\frac{5}{2}$$
3. Уравнение прямой, проходящей через вершину A и параллельной стороне BC.
Две прямые параллельные, если их угловые коэффициенты равны, т.е. \(k_{BC}=k_{A}=\frac{4}{11}\). В задаче известна одна точка и угловой коэффициент, поэтому применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении $$y-y_0=k(x-x_0)$$ Подставляем координаты точки А(-1;-1) и угловой коэффициент \(k_{A}=\frac{4}{11}\). получаем \(y+1=\frac{4}{11}(x+1) => y = \frac{4}{11}x-\frac{7}{11} \) $$ y= \frac{4}{11}x-\frac{7}{11}$$
4. Уравнение высоты AP.
Высота опущена из точки A на сторону BC, т.е. перпендикулярна этой стороне. Воспользуемся свойством угловых коэффициентов двух перпендикулярных прямых: $$k_1=-\frac{1}{k_2}$$ Найдем угловой коэффициент \(k_{AP} = -\frac{1}{k_{BC}} = -\frac{11}{4}\) Т.е известны: координата одной точки и угловой коэффициент, применим формулу уравнения прямой, проходящей через заданную точку А(-1;-1) в заданном направлении \(y +1 = -\frac{11}{4}(x+1) => y = -\frac{11}{4} x- \frac{15}{4}\) $$AP: \quad y= -\frac{11}{4} x- \frac{15}{4}$$
5. Длину высоты AP.
Длину высоты будем искать как расстояние от точки А(-1;-1) до прямой BC: \(y= \frac{4}{11}x+\frac{39}{11} => 11y - 4x - 39 = 0\) по формуле расстояния от точки до прямой $$d=|\frac{Ay_0+By_0+C}{\sqrt{A^2+B^2}}|$$ где в числителе уравнение прямой BC, в которое подставляем координаты точки A, а в знаменателе корень от суммы квадратов коэффициентов при x прямой y. Подставляем $$d=|\frac{11*(-1) - 4(-1) - 39}{\sqrt{121+16}}| =\frac{46}{\sqrt{137}}$$
6. Точку пересечения медианы BK и высоты AP.
Известны уравнения двух прямых, поэтому составим систему уравнений из этих уравнения и решим ее.
$$\begin{cases}y= \frac{5}{8}x+\frac{5}{2}\\y= -\frac{11}{4} x- \frac{15}{4}\end{cases} => \begin{cases}-\frac{11}{4} x- \frac{15}{4}= \frac{5}{8}x+\frac{5}{2}\\y= -\frac{11}{4} x- \frac{15}{4}\end{cases} => $$$$\begin{cases}\frac{27}{8} x=-\frac{25}{4}\\y= -\frac{11}{4} x- \frac{15}{4}\end{cases} => \begin{cases} x=-\frac{50}{27} \approx -1,85 \\y= \frac{145}{108} \approx 1,34\end{cases}$$
Координаты точки пересечения \(M(-\frac{50}{27}; \frac{145}{108})\)
7. Уравнение высоты CD.
Высота опущена из точки C на сторону AB, т.е. перпендикулярна этой стороне. Найдем угловой коэффициент высоты \(k_{CD} = -\frac{1}{k_{AB}} = -\frac{5}{6}\) Известны: координата одной точки С(-7;1) и угловой коэффициент, применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении \(y - 1 = -\frac{5}{6}(x+7) => y = -\frac{5}{6} x- \frac{29}{6}\) $$CD: \quad y = -\frac{5}{6} x- \frac{29}{6}$$
8. Длину высоты CD.
Длину высоты будем искать как расстояние от точки С(-7;1) до прямой AB: \(y= \frac{6}{5}x+\frac{1}{5} => 5y - 6x - 1 = 0\) Подставляем в формулу расстояния от точки до прямой и получаем $$d=|\frac{5*(-7) - 6*1 - 1}{\sqrt{25+36}}| =\frac{42}{\sqrt{61}}$$