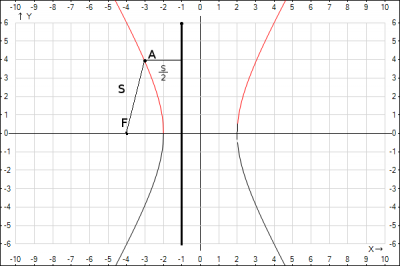
Рассмотрим рисунки, предположим, что на рисунке искомая кривая. Выберем любую точку на кривой и составим уравнение согласно условия задачи. Рассмотрим т. A(x;y). Запишем уравнение для этой точки. Расстояние от этой точки до точки F(-4;0) в декартовой системе координат равно $$S=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$ Подставляем координаты точек и получаем $$S=\sqrt{(x+4)^2+y^2}$$ Также по поводу этого расстояния от точки кривой известно, что оно в 2 раза больше, чем расстояние от точки до прямой x=-1. Расстояние от точки до прямой, которая перпендикулярна оси Ox - разность координат x точки кривой и прямой, т.е. \(S=2(x-(-1))=2(x+1)\).
Осталось приравнять это расстояния и решить уравнение $$\sqrt{(x+4)^2+y^2}=2(x+1)$$возводим в квадрат обе части уравнения $$(x+4)^2+(y)^2=4(x+1)^2 => x^2+8x+16+y^2=4x^2+8x+4$$$$y^2 -3x^2=-12 => 3x^2 - y^2=12 =>$$$$\frac{x^2}{4} - \frac{y^2}{12}=1$$Получили каноническое уравнение гиперболы. с действительной осью x (есть точки пересечения \(x = \pm 2\)) и мнимой осью y. По точкам пересечения легко проверить выполнение условия задачи.
Строим полученную гиперболу