Проведем некоторые преобразования $$ 15^х-9*5^х-3^х+9 \leq 0 => 3^х*5^х-9*5^х-3^х+9 \leq 0$$ сгруппируем члены $$5^x(3^х-9)-(3^х-9) \leq 0 => $$вынесем общий член за скобки$$(3^х-9)(5^x-1) \leq 0 => $$Найдем корни уравнения $$(3^х-9)(5^x-1) = 0 =>$$$$\begin{cases}3^х-9 =0\\ 5^x-1 =0\end{cases} => \begin{cases}3^х=3^2\\ 5^x=5^0\end{cases} => $$$$ \begin{cases}х=2\\ x=0\end{cases}$$ Наносим полученные корни на числовую ось и применяем правило змейки (см. рис) или смотрим знак произведения на каждом интервале.
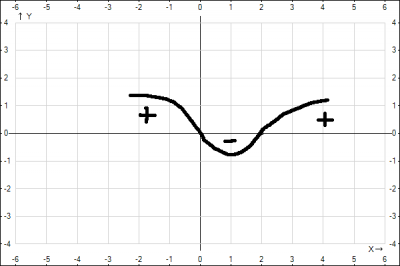
1. интервал \((2;+\infty)\), подставляем например x=3, получаем \((3^3-9)(5^3-1) > 0 \)
2. интервал \((0;2)\), подставляем например x=1, получаем \((3^1-9)(5^1-1) < 0 \)
3. интервал \((-\infty;0)\), подставляем например x=-1, получаем \((3^{-1}-9)(5^{-1}-1) > 0 \)
Ответ: \(x \in [0;2]\)



