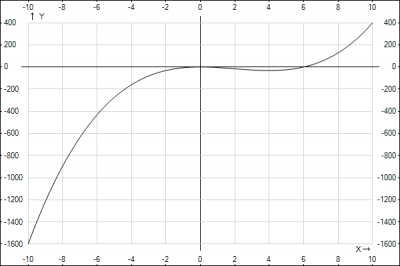
Найдем точку максимума функции.
Искать будем последующей схеме:
1. Найдем первую производную функции и приравняем ее к нулю.
$$f'(x)=(-6x^2+x^3) = -12x+3x^2$$Приравняем производную к нулю и найдем корни уравнения $$ -12x+3x^2 = 0 =>x^2 - 4x = 0 => x(x-4) = 0$$ Получили два корня (x=0; x=4) - критические точки. Определим, являются они экстремумами или точками перегиба.
2. Найдем значение производной справа и слева от критических точек. Рассмотрим три участка монотонности \((-\infty;0) \cup (0;4) \cup (4;\infty)\)
участок \((-\infty;0)\), найдем значение производной в любой точке этого участка \(f'(-1) = x(x-4) = -1*(-5) =5 > 0\) - функция возрастает
участок \( (0;4)\), найдем значение производной в любой точке этого участка \(f'(1) = x(x-4) = 1*(-3) =-3 < 0\) - функция убывает
участок \( (4;\infty)\), найдем значение производной в любой точке этого участка \(f'(5) = x(x-4) = 5*(1) =5 > 0\) - функция возрастает
3. Смотрим как меняется знак производной при переходе через критическую точку
точка x=0, слева производная больше нуля (f'(x) > 0 ), справа производная меньше 0 (f'{x} < 0 ), т.е. знак производной меняется \( + \quad 0 \quad -\), т.е. это точка локального максимума (экстремум)
точка x=4, слева производная меньше нуля (f'(x) < 0 ), справа производная больше 0 (f'{x} > 0 ), т.е. знак производной меняется \( - \quad 0 \quad +\), т.е. это точка локального минимума (экстремум)
Найдем значение функии в точке локального максимума \(f(0)=-6x^2+x^3 = -6*0^2+0^3=0 \)
Ответ: точкой локального максимума является точка с координатами (0;0)
Построим график функции и убедимся в правильности расчетов