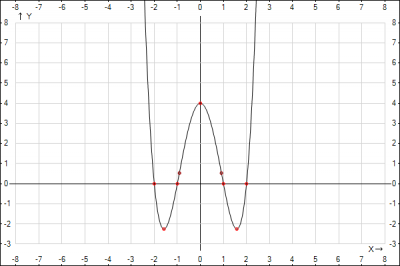
Исследуем функцию и построим график \(f(x) = x^4-5x^2+4\).
Общую схему исследования функции можно посмотреть здесь
1. Находим область определения \(x \in (-\infty;+\infty)\).
2. Находим область значения \(f(x) \in (-\infty;+\infty)\).
3. Определяем четность функции $$f(-x) = (-x)^4-5(-x)^2+4 = x^4-5x^2+4 = f(x)$$ функция четная, т.е. она симметричная относительно оси Oy. Далле будем исследовать на области \(x \in [0;+\infty)\) и воспользуемся симметрией.
4. Находим точки пересечения с осью Ox, т.е. y=0
$$x^4-5x^2+4 = 0 => x^2_{1,2} = \frac{5 \pm \sqrt{25-16}}{2} = \frac{5 \pm 3}{2} => $$$$\left[\begin{array}{c} x^2 = 4\\ x^2 = 1\end{array}\right. => \left[\begin{array}{c} x_1=2\\ x_2= -2 \\ x_3 = 1 \\ x_3 = -1 \end{array}\right.$$Координаты точек \((1;0),(2;0)\) и симметричные \((-1;0),(-2;0)\)
5. Находим точки пересечения с осью Oy, т.е. x =0
$$f(0) = x^4-5x^2+4 = 0^4-5*0^2+4 = 4$$ Координаты точки (0;4)
6. Находим интервалы возрастания и убывания функции.
Найдем первую производную $$f'(x) = (x^4-5x^2+4)' = 4x^3-10x$$Приравняем производную к нулю и найдем критические точки (или стационарные точки) $$ 4x^3-10x = 0 => x(4x^2-10) = 0 => \left[\begin{array}{c} x = 0\\ x=\sqrt{\frac{5}{2}} \approx 1.58 \\ x=-\sqrt{\frac{5}{2}} \approx -1.58 \end{array}\right. $$Т.к. функция четная рассмотрим интервалы монотонности \(x \in (0;\sqrt{\frac{5}{2}}) \cup (\sqrt{\frac{5}{2}}; +\infty)\). Для определения монотонности найдем значение производной в любой точке интервала
интервал \( (0;\sqrt{\frac{5}{2}})\) \(f'(1) = 4x^3-10x = 4*1^3-10*1 =-6 < 0 \) - функция убывает
интервал \( (\sqrt{\frac{5}{2}}; +\infty)\) \(f'(10) = 4*10^3-10*10 = 4000-100 > 0 \) - функция возрастает.
7. Классифицируем критические точки (экстремумы или точками перегиба).
Изучаем изменение монотонности (знака производной) при переходе через критическую точку.
точка \(x=0\), из симметрии видно, что слева производная больше нуля \(f'(x) > 0 \) возрастает, справа меньше нуля \(f'(x) < 0 \) убывает, т.е. знак меняется \(+\quad 0\quad -\) - точка локального максимума (экстремум).Точка локального максимума имеет координаты (0;4)
точка \(x=\sqrt{\frac{5}{2}}\), слева производная меньше нуля \(f'(x) < 0 \) функция убывает , справа производная больше нуля \(f'(x) > 0 \) функция возрастает, т.е. знак меняется \(-\quad 0\quad +\) - точка локального минимума (экстремум). Находим значение функции в этой точке \(f(\sqrt{\frac{5}{2}}) = (\sqrt{\frac{5}{2}})^4-5(\sqrt{\frac{5}{2}})^2+4 = -\frac{9}{4}\). Точка локального минимума имеет координаты \((\sqrt{\frac{5}{2}};-\frac{9}{4})\)
8. Выпуклость. Находим интервалы выпуклости и точки перегиба.
Для этого найдем вторую производную $$f''(x) = (4x^3-10x)' = 12x^2-10$$ Приравняем вторую производную к нулю $$12x^2-10 = 0 => x = \pm \sqrt{\frac{5}{6}} \approx \pm 0,91$$В силу симметрии рассматривать выпуклость будет на интервале \(x \in (0;\sqrt{\frac{5}{6}}) \cup (\sqrt{\frac{5}{6}};+\infty)\).
найдем значение функции в этой точке \(f(\sqrt{\frac{5}{6}}) = (\sqrt{\frac{5}{6}})^4-5(\sqrt{\frac{5}{6}})^2+4= \frac{19}{36}\).
Находим значения второй производной на интервалах выпуклости и определяем выпуклость графика функции:
интервал \((0;\sqrt{\frac{5}{6}})\). \(f''(0,1) = 12*0.1^2-10 < 0 \) график функции имеет выпуклость вверх (выпуклый).
интервал \((\sqrt{\frac{5}{6}}; +\infty)\). \(f''(1) = 12*1^2-10 > 0 \) график функции имеет выпуклость вниз (вогнутый).
Получили, что при переходе через точку \(x= \sqrt{\frac{5}{6}}\) вторая производная меняет знак (выпуклость), т.е это точка перегиба. Координаты точки перегиба \((\sqrt{\frac{5}{6}};\frac{19}{36})\)
9. Строим график функции в правой полуплоскости и симметрично отображаем его в левую полуплоскость и получаем следующий график