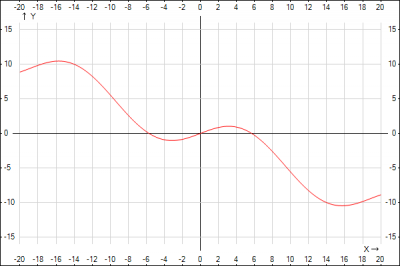
Найти точки экстремума функции \( f(x)=3\sin(\frac{x}{3}) -0,5x\).
Задачу будем решать по следующей схеме:
1. Найдем критические точки - точки экстремума (максимума и минимума) и точки перегиба,
для этого найдем первую производную и приравняем ее к нулю, т.е. получим участки монотонности функции, где корни уравнения являются границами этих участков.
$$ f'(x)=(3\sin(\frac{x}{3}) -0,5x)' = 3\cos(\frac{x}{3})*\frac{1}{3} - 0,5 = \cos(\frac{x}{3})- 0,5$$Приравняем первую производную к 0 $$ \cos(\frac{x}{3})- 0,5 = 0 => \cos(\frac{x}{3}) = 0,5 => \frac{1}{3}x = \pm \frac{\pi}{3} + 2\pi n =>$$$$x = \pm \pi + 6\pi n$$
2. Определим знак производной на каждом участке монотонности. Т.к. функция периодическая, то рассмотрим три участка одного периода \((-5\pi;-\pi) \cup (-\pi;\pi) \cup (\pi; 5\pi)\)
на участке \((-5\pi;-\pi)\) берем любую точку и находим значение производной в этой точке \(f'(-3\pi) = \cos(\frac{-3\pi}{3}) - 0,5 = -1 -0.5 = -1.5 < 0\)
на участке \((-\pi;\pi)\) берем любую точку и находим значение производной в этой точке \(f'(0) = \cos(\frac{0}{3}) - 0,5 = 1 -0.5 = 0.5 > 0\)
на участке \((\pi; 5\pi)\) берем любую точку и находим значение производной в этой точке \(f'(3\pi) = \cos(\frac{3\pi}{3}) - 0,5 = -1 -0.5 = -1.5 < 0\)
3. Смотрим изменение знака производной при переходе через критическую точку
точка \(-\pi\) . Слева производная меньше 0, а справа больше нуля, т.е. получаем \(- \quad 0 \quad +\) это точка локального минимума (экстремум)
точка \(\pi\) . Слева производная больше 0 , а справа меньше нуля, т.е. получаем \(+\quad 0 \quad -\) это точка локального максимума (экстремум)
Получили, что все критические точки являются экстремумами \(x = \pm \pi + 6\pi n\)
Построим график и убедимся в истинности расчетов.