Уравнение касательной находится по формуле $$y = f(x_0)+f'(x_0)(x-x_0) \quad (1)$$
1. \(f(x_0)\) - значение функции в точке касания, найдем его \(f(1) =\frac{1-1}{1+1}=0\)
2. \(f'(x_0)\) - первая производная функции в точке касания. Найдем первую производную $$f'(1) =(\frac{х-1}{х+1})'=\frac{x+1-x+1}{(x+1)^2}=\frac{2}{(x+1)^2}=\frac{2}{(1+1)^2}=\frac{1}{2}$$
3. Подставляем полученные данные в (1), получаем $$y = f(x_0)+f'(x_0)(x-x_0) = 0 + \frac{1}{2}(x-1) =>$$$$y= \frac{1}{2}(x-1)$$Это и есть уравнение касательной к графику функции в заданную точку касания.
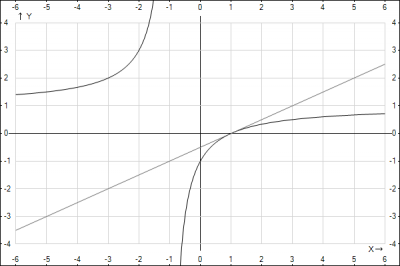
Смотрим рисунок.