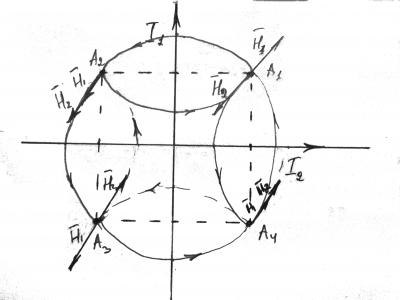
В задаче не сказано о расположении точки A, поэтому рассмотрим 4 случая. Вспомним формулу для расчета вектора магнитной индукции $$\vec{B}=\mu \mu_0 \vec{H}$$где \(\vec{H}\) - напряженность магнитного поля в точке, которая для прямолинейного бесконечного проводника с током равна $$H=\frac{I}{2\pi a}$$где a - расстояние до проводника, в задаче оно везде одинаковое, \(I=I_1=I_2\) - сила тока.
Построим векторы напряженности поля в каждой точке \(A_1;A_2;A_3;A_4\). Направление вектора напряженности \(\vec{H}\) определяем по правилу правой руки (большой палец правой руки ставим по направления тока, согнутые четыре пальца покажут направление силовой линии вектора ).
Рассмотрим поле в точках:
точка \(A_1\):
\(\vec{H}=\vec{H_1}+\vec{H_2}\), где \(\vec{H_1}\) - вектор напряженности поля, создаваемое током \(I_1\), \(\vec{H_2}\) - вектор напряженности поля, создаваемое током \(I_2\). Проецируя на ось Ox получаем $$\vec{H}=\vec{H_1}-\vec{H_2} = \frac{I_1}{2\pi a}-\frac{I_2}{2\pi a}=0$$
точка \(A_3\):
\(\vec{H}=\vec{H_1}+\vec{H_2}\). Проецируя на ось Ox получаем $$\vec{H}=\vec{H_2}-\vec{H_1} = \frac{I_2}{2\pi a}-\frac{I_1}{2\pi a}=0$$
точка \(A_2\):
\(\vec{H}=\vec{H_1}+\vec{H_2}\), где \(\vec{H_1}\). Проецируя на ось Ox получаем $$\vec{H}=-\vec{H_1}-\vec{H_2} = -\frac{I_1}{2\pi a}-\frac{I_2}{2\pi a}=-\frac{I}{\pi a}$$
точка \(A_4\): \(\vec{H}=\vec{H_1}+\vec{H_2}\). Проецируя на ось Ox получаем $$\vec{H}=\vec{H_1}+\vec{H_2} = \frac{I_1}{2\pi a}+\frac{I_2}{2\pi a}=\frac{I}{\pi a}$$
Получили, что в точках \(A_1;A_3\) - напряженность равна 0,т.е. вектор магнитной индукции также равен нулю. В точках \(A_2;A_4\) - напряженности равны по модулю, т.е. вектор магнитной индукции равны по модулю и противонаправленный.
Рассчитаем их:
точка \(A_2\):
\(B= -\mu \mu_0*H= -\mu \mu_0*\frac{I}{ \pi a}=-1*4 \pi *10^{-7}\frac{H}{A^2}*\frac{10A}{ \pi *1M}=-4*10^{-6} \frac{H}{AM}=-4*10^{-6}T\)
точка \(A_4\):
\(B= \mu \mu_0*H= \mu \mu_0*\frac{I}{ \pi a}=1*4 \pi *10^{-7}\frac{H}{A^2}*\frac{10A}{ \pi *1M}=4*10^{-6} \frac{H}{AM}=4*10^{-6}T\)