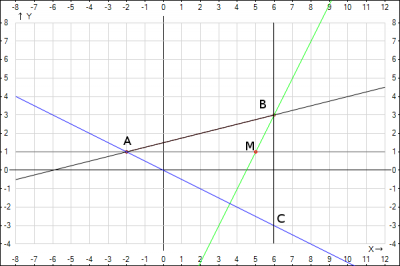
1. Уравнение прямой AB
Две вершины есть, т.е. уравнение одной стороны можно получить как уравнение прямой, проходящей через две заданные точки $$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}$$Подставляем координаты вершин А(-2,1) В(6;3) в уравнение и получаем $$\frac{x+2}{6+2}=\frac{y-1}{3-1} =>y=\frac{1}{4}x+\frac{3}{2}$$
Для того, чтобы найти уравнения оставшихся сторон,
найдем уравнение высот:
2. проходящей через вершину A и перпендикулярную BC, назовем ее AM. Две точки у нас известны, применим уравнение прямой проходящей через две заданные точки А(-2,1), M(5;1) $$\frac{x+2}{5+2}=\frac{y-1}{1-1} $$Т.к. в знаменателе y у нас 0, значит прямая параллельна оси Ox и ее уравнение \(y=1\)
3. проходящей через вершину B и перпендикулярную AC, назовем ее BM. Две точки у нас известны, применим уравнение прямой проходящей через две заданные точки В(6;3), M(5;1) $$\frac{x-6}{5-6}=\frac{y-3}{1-3} =>y=2x-9$$
Уравнения этих высот мы искали только для одного: как известно угловые коэффициенты перпендикулярных прямых связаны следующим соотношением \(k_1=-\frac{1}{k_2}\), т.е. для уравнений двух оставшихся сторон у нас есть по одной вершине и угловые коэффициенты. Получим эти уравнения:
4. Уравнение прямой AC. Для этого уравнения у нас есть координаты вершины А(-2,1) и найдем угловой коэффициент, зная угловой коэффициент перпендикулярной прямой BM, который равен \(k_{BM} = 2\) =>\(k_{AC} = -\frac{1}{k_{BM}}=-\frac{1}{2}\). Тогда уравнение прямой AC равно $$y-1=-\frac{1}{2}(x+2) =>y = -\frac{1}{2}x$$
5. Уравнение прямой BC. Известно, что высота AM перпендикулярная этой стороне параллельна оси Ox, значит эта сторона будет параллельна оси Oy и при этом проходить через вершину В(6;3), т.е. ее уравнение будет \(x=6\)
Уравнения трех прямых сторон треугольника найдены. Постоим треугольник